题目内容
【题目】机器人![]() (阿法狗)在下围棋时,令人称道的算法策略是:每一手棋都能保证在接下来的十几步后,局面依然是满意的.这种策略给了我们启示:每一步相对完美的决策,对最后的胜利都会产生积极的影响.
(阿法狗)在下围棋时,令人称道的算法策略是:每一手棋都能保证在接下来的十几步后,局面依然是满意的.这种策略给了我们启示:每一步相对完美的决策,对最后的胜利都会产生积极的影响.
下面的算法是寻找“![]() ”中“比较大的数
”中“比较大的数![]() ”,现输入正整数“42,61,80,12,79,18,82,57,31,18“,从左到右依次为
”,现输入正整数“42,61,80,12,79,18,82,57,31,18“,从左到右依次为![]() ,其中最大的数记为
,其中最大的数记为![]() ,则
,则![]() ( )
( )
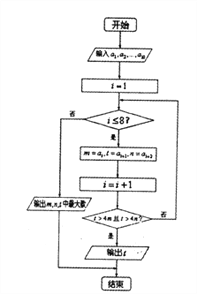
A. 0 B. 1 C. 2 D. 3
【答案】D
【解析】模拟程序框图的运行过程,可得:
i=1
m=42,t=61,n=80
i=2
不满足条件t>4m且t>4n,m=61,t=80,n=12,i=3
不满足条件t>4m且t>4n,m=80,t=12,n=79,i=4
不满足条件t>4m且t>4n,m=12,t=79,n=18,i=5
满足条件t>4m且t>4n,结束,输出t的值为79.
由于最大的数记为T的值为82,
则Tt=8279=3.
故选:D.

【题目】生产甲乙两种元件,其质量按检测指标划分为:指标大于或者等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
测试指标 |
|
|
|
|
|
元件甲 | 8 | 12 | 40 | 32 | 8 |
元件乙 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计元件甲、乙为正品的概率;
(2)生产一件元件甲,若是正品可盈利40元,若是次品则亏损5元,生产一件元件乙,若是正品可盈利50元,若是次品则亏损10元.在(1)的前提下:
(i)记![]() 为生产1件甲和1件乙所得的总利润,求随机变量
为生产1件甲和1件乙所得的总利润,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(ii)求生产5件元件乙所获得的利润不少于140元的概率.
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
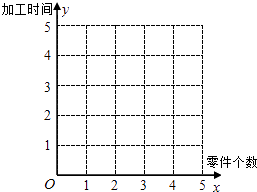
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少时间? 参考公式:回归直线 ![]() =bx+a,其中b=
=bx+a,其中b= 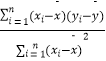 =
= 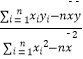 ,a=
,a= ![]() ﹣b
﹣b ![]() .
.