题目内容
【题目】已知函数![]() ,其中常数
,其中常数![]() .
.
(1)若![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(2)令![]() ,将函数
,将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数![]() 的图象.区间
的图象.区间![]() 满足:
满足:![]() 在
在![]() 上至少含有30个零点.在所有满足上述条件的
上至少含有30个零点.在所有满足上述条件的![]() 中,求
中,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】(1)因为函数y=f(x)在![]() 上单调递增,且
上单调递增,且![]() ,
,
所以![]() ,且
,且![]() ,
,
所以![]() .即
.即![]() 的取值范围是
的取值范围是![]() .
.
(2)![]() ,
,
将![]() 的图象向左平移
的图象向左平移![]() 个单位,再向上平移1个单位后得到
个单位,再向上平移1个单位后得到![]() 的图象,所以
的图象,所以![]() .
.
令![]() ,得
,得![]() 或
或![]() ,
,
所以两个相邻零点之间的距离为![]() 或
或![]() .
.
若b-a最小,则a和b都是零点,
此时在区间[a,π+a],[a,2π+a],…,[a,mπ+a](m∈N*)上分别恰有3,5,…,2m+1个零点,所以在区间[a,14π+a]上恰有29个零点,
从而在区间(14π+a,b]上至少有一个零点,
所以![]() .
.
另一方面,在区间![]() 上恰有30个零点,
上恰有30个零点,
因此,b-a的最小值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少时间? 参考公式:回归直线 ![]() =bx+a,其中b=
=bx+a,其中b= 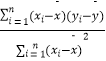 =
= 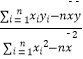 ,a=
,a= ![]() ﹣b
﹣b ![]() .
.