题目内容
【题目】f(x)=lnx﹣ax+1.
(1)求f(x)的单调增区间.
(2)求出f(x)的极值.
【答案】
(1)解:f′(x)= ![]() ﹣a(x>0)
﹣a(x>0)
∴当a≤0时f′(x)>0恒成立,
∴f(x)的增区间为(0,+∞),
当a>0时,f′(x)>0的解为(0, ![]() ),
),
∴f(x)的增区间为(0, ![]() )
)
(2)解:f′(x)= ![]() ﹣a=0解得:x=
﹣a=0解得:x= ![]() ,
,
∴a>0时,x∈( ![]() ,+∞)时,f′(x)<0,
,+∞)时,f′(x)<0,
x∈(0, ![]() )时,f′(x)>0,
)时,f′(x)>0,
∴x= ![]() 是f(x)的极大值无极小值,
是f(x)的极大值无极小值,
当a≤0时,f′(x)>0恒成立,无极值
【解析】(1)求出函数的导数,通过讨论a的范围,求出函数的递增区间;(2)求出函数的导数,通过讨论a的范围,求出函数的单调区间,从而求出函数的极值.
【考点精析】关于本题考查的利用导数研究函数的单调性和函数的极值与导数,需要了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能得出正确答案.
是极小值才能得出正确答案.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少时间? 参考公式:回归直线 ![]() =bx+a,其中b=
=bx+a,其中b= 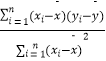 =
= 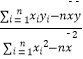 ,a=
,a= ![]() ﹣b
﹣b ![]() .
.


