题目内容
在△ABC中,∠ABC=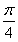 ,AB=
,AB=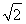 ,BC=3,则sin∠BAC=( )
,BC=3,则sin∠BAC=( )
A. 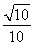 B.
B.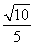 C.
C.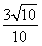 D.
D.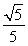
C
【解析】由余弦定理可得AC=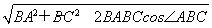
=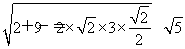 ,于是由正弦定理可得
,于是由正弦定理可得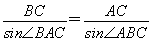 ,于是sin∠BAC=
,于是sin∠BAC=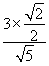 =
=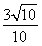

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
题目内容
在△ABC中,∠ABC=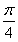 ,AB=
,AB=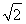 ,BC=3,则sin∠BAC=( )
,BC=3,则sin∠BAC=( )
A. 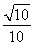 B.
B.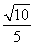 C.
C.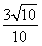 D.
D.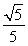
C
【解析】由余弦定理可得AC=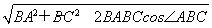
=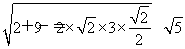 ,于是由正弦定理可得
,于是由正弦定理可得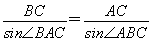 ,于是sin∠BAC=
,于是sin∠BAC=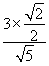 =
=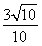

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案