ĢāÄæÄŚČŻ
”¾ĢāÄæ”æijŹŠµēŹÓĢØĪŖĮĖŠū“«£¬¾Ł°ģĪŹ“š»ī¶Æ£¬Ė껜¶ŌøĆŹŠ15ÖĮ65ĖźµÄČĖČŗ½ųŠŠ³éŃł£¬ĘµĀŹ·Ö²¼Ö±·½Ķ¼¼°»Ų“šĪŹĢāĶ³¼Ę½į¹ūČē±ķĖłŹ¾£ŗ
×éŗÅ | ·Ö×é | »Ų“šÕżČ· | »Ų“šÕżČ·µÄČĖŹż |
µŚ1×é | [15£¬25£© | 5 | 0.5 |
µŚ2×é | [25£¬35£© | a | 0.9 |
µŚ3×é | [35£¬45£© | 27 | x |
µŚ4×é | [45£¬55£© | b | 0.36 |
µŚ5×é | [55£¬65£© | 3 | y |
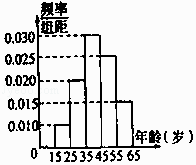
£Ø1£©·Ö±šĒó³öa£¬b£¬x£¬yµÄÖµ£»
£Ø2£©“ÓµŚ2£¬3£¬4×é»Ų“šÕżČ·µÄČĖÖŠÓĆ·Ö²ć³éŃłµÄ·½·Ø³éČ”6ČĖ£¬ŌņµŚ2£¬3£¬4×éĆæ×éÓ¦ø÷³éČ”¶ąÉŁČĖ£æ
£Ø3£©ŌŚ£Ø2£©µÄĒ°ĢįĻĀ£¬µēŹÓĢؾö¶ØŌŚĖł³éČ”µÄ6ČĖÖŠĖ껜³éČ”3ČĖ°ä·¢ŠŅŌĖ½±£¬Ēó£ŗĖł³éČ”µÄČĖÖŠµŚ3×éÖĮÉŁÓŠ1ČĖ»ńµĆŠŅŌĖ½±µÄøÅĀŹ£®
”¾“š°ø”æ
£Ø1£©½ā£ŗµŚ1×éČĖŹż5”Ā0.05=100£¬
ĖłŅŌn=100”Ā0.1=1000£¬
µŚ2×éČĖŹż1000”Į0.2=200£¬ĖłŅŌa=200”Į0.9=180£¬
µŚ3×éČĖŹż1000”Į0.3=300£¬ĖłŅŌx=270”Ā300=0.9£¬
µŚ4×éČĖŹż1000”Į0.25=250£¬ĖłŅŌb=250”Į0.36=90£¬
µŚ5×éČĖŹż1000”Į0.15=150£¬ĖłŅŌy=3”Ā150=0.02
£Ø2£©½ā£ŗµŚ2£¬3£¬4×é»Ų“šÕżČ·µÄČĖµÄ±ČĪŖ180£ŗ270£ŗ90=2£ŗ3£ŗ1£¬
“ÓµŚ2£¬3£¬4×é»Ų“šÕżČ·µÄČĖÖŠÓĆ·Ö²ć³éŃłµÄ·½·Ø³éČ”6ČĖ£¬
ĖłŅŌµŚ2£¬3£¬4×éĆæ×éÓ¦ø÷ŅĄ“Ī³éČ”2ČĖ£¬3ČĖ£¬1ČĖ
£Ø3£©½ā£ŗ¼Ē³éČ”µÄ6ČĖÖŠ£¬µŚ2×éµÄ¼ĒĪŖa1£¬a2£¬µŚ3×éµÄ¼ĒĪŖb1£¬b2£¬b3£¬µŚ4×éµÄ¼ĒĪŖc£¬
Ōņ“Ó6Ćūѧɜ֊ČĪČ”3ĆūµÄĖłÓŠæÉÄܵÄĒéæöÓŠ20ÖÖ£¬ĖüĆĒŹĒ£ŗ 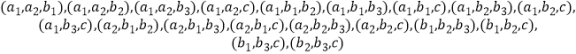
ĘäÖŠ¼Ē”°µŚ3×éÖĮÉŁÓŠ1ČĖ”±ĪŖŹĀ¼žA£¬ŌņAµÄ¶ŌĮ¢ŹĀ¼žŹĒ”°µŚ3×éµÄƻӊєµ½”±£¬
Ę仳±¾ŹĀ¼žøöŹżŹĒ1øö£¬¼“£Øa1£¬a2£¬c£©£¬
¹ŹĖł³éČ”µÄČĖÖŠµŚ3×éÖĮÉŁÓŠ1ČĖ»ńµĆŠŅŌĖ½±µÄøÅĀŹĪŖ ![]()
”¾½āĪö”æ£Ø1£©ĻČĒó³öµŚ1×éČĖŹżĪŖ100£¬“Ó¶ųµĆµ½n=1000£¬ÓÉ“ĖÄÜĒó³öĒó³öa£¬b£¬x£¬yµÄÖµ£®£Ø2£©µŚ2£¬3£¬4×é»Ų“šÕżČ·µÄČĖµÄ±ČĪŖ2£ŗ3£ŗ1£¬ÓÉ“ĖÄÜĒó³öµŚ2£¬3£¬4×éĆæ×éÓ¦ø÷³éČ”µÄČĖŹż£®£Ø3£©¼Ē³éČ”µÄ6ČĖÖŠ£¬µŚ2×éµÄ¼ĒĪŖa1 £¬ a2 £¬ µŚ3×éµÄ¼ĒĪŖb1 £¬ b2 £¬ b3 £¬ µŚ4×éµÄ¼ĒĪŖc£¬ÓÉ“ĖĄūÓĆĮŠ¾Ł·ØÄÜĒó³öĖł³éČ”µÄČĖÖŠµŚ3×éÖĮÉŁÓŠ1ČĖ»ńµĆŠŅŌĖ½±µÄøÅĀŹ£®
”¾æ¼µć¾«Īö”æ±¾ĢāÖ÷ŅŖæ¼²éĮĖʵĀŹ·Ö²¼Ö±·½Ķ¼µÄĻą¹ŲÖŖŹ¶µć£¬ŠčŅŖÕĘĪÕʵĀŹ·Ö²¼±ķŗĶʵĀŹ·Ö²¼Ö±·½Ķ¼£¬ŹĒ¶ŌĻąĶ¬Źż¾ŻµÄĮ½ÖÖ²»Ķ¬±ķ“ļ·½Ź½.ÓĆ½ō“յıķøńøı䏿¾ŻµÄÅÅĮŠ·½Ź½ŗĶ¹¹³ÉŠĪŹ½£¬æÉÕ¹Ź¾Źż¾ŻµÄ·Ö²¼Ēéæö.Ķعż×÷Ķ¼¼ČæÉŅŌ“ÓŹż¾ŻÖŠĢįČ”ŠÅĻ¢£¬ÓÖæÉŅŌĄūÓĆĶ¼ŠĪ“«µŻŠÅĻ¢²ÅÄÜÕżČ·½ā“š“ĖĢā£®