题目内容

已知m∈R，则动圆x2+y2+4mx-2my+6m2-4=0的圆心的轨迹方程为______．
动圆x2+y2+4mx-2my+6m2-4=0可化为（x+2m）2+（y-m）2=4-m2，
∴圆心的坐标为（-2m，m），半径r=
4-m2
（-2＜m＜2）．
设圆心的坐标为（x，y），则x+2y=0（-4＜x＜4）．
故答案为：x+2y=0（-4＜x＜4）．
练习册系列答案
相关题目
已知定点A（-2，0），B（2，0），及定点F（1，0），定直线l：x=4，不在x轴上的动点M到定点F的距离是它到定直线l的距离的
1
2
倍，设点M的轨迹为E，点C是轨迹E上的任一点，直线AC与BC分别交直线l与点P，Q．
（1）求点M的轨迹E的方程；
（2）试判断以线段PQ为直径的圆是否经过定点F，并说明理由．
已知直线l：xcosθ+ysinθ=1，且0P⊥l于P，O为坐标原点，则点P的轨迹方程为（　　）
A．x2+y2=1B．x2-y2=1C．x+y=1D．x-y=1
（Ⅰ）求与x轴相切，圆心在直线3x-y=0上，且被直线x-y=0截得的弦长为2
7
的圆的方程．
（Ⅱ）设定点M（-3，4），动点N在圆x2+y2=4上运动，以OM、ON为两边作平行四边形MONP，求点P的轨迹．
已知一个圆的圆心为坐标原点，半径为2．从这个圆上任意一点P向x轴作垂线段PP′，求线段PP′中点M的轨迹．
如图，梯形ABCD中，AB∥CD，且AB⊥平面α，AB=2BC=2CD=4，点P为α内一动点，且∠APB=∠DPC，则P点的轨迹为（　　）
A．直线B．圆C．椭圆D．双曲线
已知动圆过定点Q（1，0），且与定直线x=-1相切．
（1）求此动圆圆心P的轨迹C的方程；
（2）若过点M（4，0）的直线l与曲线C分别相交于A，B两点，若2
AM
=
MB
，求直线l的方程．
已知圆A：（x+2）2+y2=36，圆A内一定点B（2，0），圆P过B点且与圆A内切，则圆心P的轨迹为（　　）
A．圆B．椭圆C．直线D．以上都不对
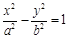双曲线与椭圆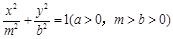的离心率互为倒数，则（　　）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网