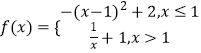题目内容
【题目】函数 f(x)=2x﹣ ![]() 的定义域为(0,1](a为实数).
的定义域为(0,1](a为实数).
(Ⅰ)当a=﹣1时,求函数y=f(x)的值域;
(Ⅱ)若函数y=f(x)在定义域上是减函数,求a的取值范围;
(Ⅲ)求函数y=f(x)在x∈(0,1]上的最大值及最小值,并求出函数取最值时x的值.
【答案】解:(Ⅰ)显然函数y=f(x)的值域为 ![]() ;
;
(Ⅱ)若函数y=f(x)在定义域上是减函数,则:f'(x)=2+![]()
![]() 0
0![]() a
a![]() a--2x2
a--2x2![]() 在定义域上恒成立
在定义域上恒成立
而﹣2x2∈[﹣2,0)
∴a≤﹣2
(II)当a≥0时,函数y=f(x)在(0.1]上单调递增,无最小值,
当x=1时取得最大值2﹣a;
由(2)得当a≤﹣2时,函数y=f(x)在(0.1]上单调递减,无最大值,
当x=1时取得最小值2﹣a;
当﹣2<a<0时,函数y=f(x)在 ![]() 上单调递减,在
上单调递减,在 ![]() 上单调递增,无最大值,
上单调递增,无最大值,
当 ![]() 时取得最小值
时取得最小值 ![]()
【解析】(1)a=﹣1时,函数为对勾函数,结合函数图像可直接写出函数的值域.
(2)函数y=f(x)在定义域上是减函数,则 f '( x ) ![]() 0,再进行分离变量进行求解.
0,再进行分离变量进行求解.
(3)对a进行分情况讨论,结合函数的单调性求解函数的最值.
【考点精析】根据题目的已知条件,利用函数的值域和函数的最大(小)值与导数的相关知识可以得到问题的答案,需要掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目