题目内容
16.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+1,x≥0}\\{x+1,x<0}\end{array}\right.$,则满足不等式f(x2-3)>f(2x)的x的取值范围是(-∞,-1)∪(3,+∞).分析 根据分段函数的单调性进行求解即可.
解答 解:∵f(x)=$\left\{\begin{array}{l}{{x}^{2}+1,x≥0}\\{x+1,x<0}\end{array}\right.$,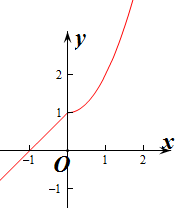
∴函数f(x)在(-∞,+∞)上为增函数,
则由f(x2-3)>f(2x)得x2-3>2x,
即x2-2x-3>0,
解得x>3或x<-1,
即x的取值范围是(-∞,-1)∪(3,+∞),
故答案为:(-∞,-1)∪(3,+∞)
点评 本题主要考查不等式的求解,结合函数单调性的性质是解决本题的关键.

练习册系列答案
相关题目
6.在数列{an}中,a1=2,an+1=an+ln(1+$\frac{1}{n}$),则a5=( )
| A. | 1+ln2 | B. | 2+ln3 | C. | 3+ln5 | D. | 2+ln5 |
4.讲一个球的体积扩大1倍,则扩大后球的半径是原球半径的( )
| A. | 1倍 | B. | 2倍 | C. | $\root{3}{2}$倍 | D. | $\sqrt{3}$倍 |