题目内容
【题目】如图，矩形
垂直于正方形
垂直于平面
．且
．
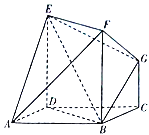
（1）求三棱锥
的体积；
（2）求证：面
面
．
【答案】（Ⅰ）
；（Ⅱ）详见解析.
【解析】
（1）因为面
面
，
面
面
，
所以
又因为
面，故
，
因为
，
所以
即三棱锥
的高，
因此三棱锥的体积
（2）如图，设
的中点为
，连结
．
在
中可求得
；
在直角梯形
中可求得
；
在
中可求得
从而在等腰
，等腰
中分别求得
，
此时在
中有
，
所以
因为是等腰底边中点，所以
，
所以
，
因此面
面
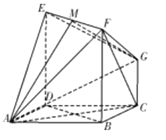
【方法点晴】
本题主要考查的是线面垂直和面面垂直的判定定理和性质定理，属于中档题．再立体几何中如果题目条件中有面面垂直，则必然会用到面面垂直的性质定理，即由面面垂直得线面垂直；证明线面垂直的关键是证明线线垂直，证明线线垂直常用的方法是直角三角形、等腰三角形的“三线合一”和菱形、正方形的对角线．本题用到了直角三角形．
【题目】某公司为提高市场销售业绩，设计了一套产品促销方案，并在某地区部分营销网点进行试点.运作一年后，对“采取促销”和“没有采取促销”的营销网点各选了50个，对比上一年度的销售情况，分别统计了它们的年销售总额，并按年销售总额增长的百分点分成5组：
，
，
，
，
，分别统计后制成如图所示的频率分布直方图，并规定年销售总额增长10个百分点及以上的营销网点为“精英店”.
“采用促销”的销售网点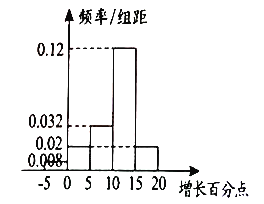
“不采用促销”的销售网点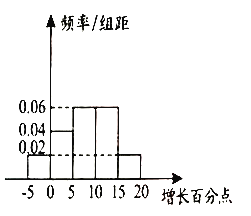
（1）请根据题中信息填充下面的列联表，并判断是否有
的把握认为“精英店与采促销活动有关”；
采用促销 | 无促销 | 合计 | |
精英店 | |||
非精英店 | |||
合计 | 50 | 50 | 100 |
（2）某“精英店”为了创造更大的利润，通过分析上一年度的售价
（单位：元）和日销量
（单位：件）（
）的一组数据后决定选择
作为回归模型进行拟合.具体数据如下表，表中的
|
|
|
|
|
|
|
45.8 | 395.5 | 2413.5 | 4.6 | 21.6 |
|
|
①根据上表数据计算
，
的值；
②已知该公司产品的成本为10元/件，促销费用平均5元/件，根据所求出的回归模型，分析售价
定为多少时日利润
可以达到最大.
附①：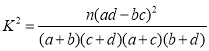
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
附②：对应一组数据
，
其回归直线
的斜率和截距的最小二乘法估计分别为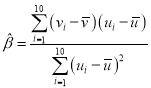
，
.
