题目内容
【题目】已知函数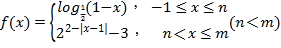
的值域是
，有下列结论：①当
时，
； ②当
时，
；③当
时，
； ④当时，
．其中结论正确的所有的序号是( )．
A.①②B.③④C.②③D.②④
【答案】C
【解析】
根据函数函数的单调性及分段函数的定义，画出函数图象，根据图象即可求得答案．
解：当x＞1时，x﹣1＞0，f（x）＝22﹣x+1﹣3＝23﹣x﹣3，单调递减，
当﹣1＜x＜1时，f（x）＝22+x﹣1﹣3＝21+x﹣3，单调递增，
∴
在（﹣1，1）单调递增，在（1，+∞）单调递减，
∴当x＝1时，取最大值为1，
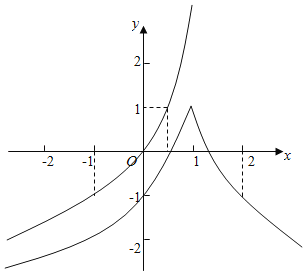
∴绘出的图象，如图下方曲线：
①当n＝0时，f（x）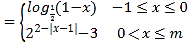
，
由函数图象可知：
要使f（x）的值域是[﹣1，1]，
则m∈（1，2]；故①错误；
②当
时，f（x）
，
f（x）在[﹣1，
]单调递增，f（x）的最大值为1，最小值为﹣1，
∴
；故②正确；
③当
时，m∈[1，2]；故③正确，④错误，
故选：C．
练习册系列答案
相关题目
