题目内容
直线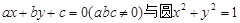 相离,若
相离,若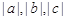 能表示为某三角形的三条边长,则根据已知条件能够确定该三角形的形状是____________.
能表示为某三角形的三条边长,则根据已知条件能够确定该三角形的形状是____________.
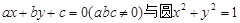 相离,若
相离,若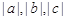 能表示为某三角形的三条边长,则根据已知条件能够确定该三角形的形状是____________.
能表示为某三角形的三条边长,则根据已知条件能够确定该三角形的形状是____________. 钝角三角形
试题分析: 因为直线
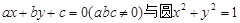 相离,那么根据点到直线的距离公式可知,
相离,那么根据点到直线的距离公式可知,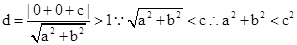 ,由此结合三角形的余弦定理可知,
,由此结合三角形的余弦定理可知,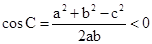 ,可知该三角形为钝角三角形。答案为钝角三角形。
,可知该三角形为钝角三角形。答案为钝角三角形。点评:解决该试题的关键是利用点到直线的距离公式得到a,b,c,的关系式,进而利用余弦定理来判定三角形的形状。

练习册系列答案
相关题目
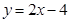 绕着其与
绕着其与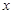 轴的交点逆时针旋转
轴的交点逆时针旋转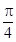 得到直线m,则m与圆
得到直线m,则m与圆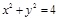 截得弦长为( )
截得弦长为( )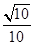
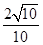
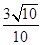
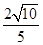
 ,则直线
,则直线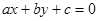 被圆
被圆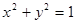 所截得的弦长为( )
所截得的弦长为( ) 

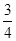
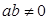 ,点
,点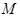
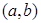 是圆
是圆 内一点,直线
内一点,直线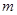 是以点
是以点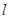 的方程是
的方程是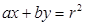 ,则下列结论正确的是( )
,则下列结论正确的是( )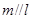 ,且
,且 ,且
,且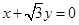 绕原点按顺时针方向旋转
绕原点按顺时针方向旋转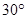 所得直线与圆
所得直线与圆 的位置关系是( ).
的位置关系是( ). 的位置关系是
的位置关系是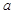 为任意实数时,直线
为任意实数时,直线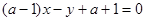 恒过定点
恒过定点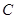 ,则以
,则以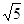 为半径的圆的方程是_____________.
为半径的圆的方程是_____________.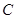 经过
经过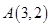 、
、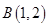 两点,且圆心在直线
两点,且圆心在直线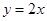 上.
上. 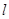 经过点
经过点