题目内容
(本小题满分13分)已知圆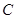 经过
经过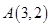 、
、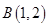 两点,且圆心在直线
两点,且圆心在直线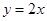 上.
上.
(Ⅰ)求圆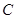 的方程;
的方程;
(Ⅱ)若直线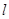 经过点
经过点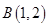 且与圆
且与圆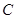 相切,求直线
相切,求直线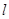 的方程.
的方程.
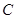 经过
经过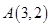 、
、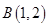 两点,且圆心在直线
两点,且圆心在直线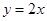 上.
上. (Ⅰ)求圆
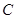 的方程;
的方程; (Ⅱ)若直线
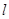 经过点
经过点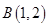 且与圆
且与圆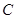 相切,求直线
相切,求直线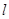 的方程.
的方程.(Ⅰ)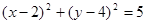 . (Ⅱ)
. (Ⅱ) 。
。
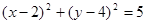 . (Ⅱ)
. (Ⅱ) 。
。本试题主要是考查了直线与圆的位置关系的运用。
(1)设圆C的方程为(x-a)2+(y-b)2=r2,r>0,,依题意得: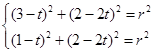
,解出待定系数,可得圆 C的方程.(2)当直线l的斜率存在时,可设直线l的方程,由圆心到直线的距离等于半径解出k值,从而得到直线l的方程.
解:(Ⅰ)方法1:设所求圆的方程为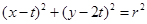 .依题意,可得………2分
.依题意,可得………2分
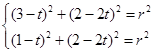 ,……………………4分
,……………………4分
解得
∴所求圆的方程为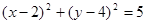 .…………………7分
.…………………7分
方法2:由已知,AB的中垂线方程为: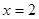 . …………………2分
. …………………2分
由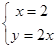 得
得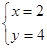 .所求圆的圆心为C(2,4).…………………………2分
.所求圆的圆心为C(2,4).…………………………2分
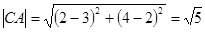 .
.
∴所求圆的方程为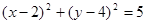 .……………………7分
.……………………7分
(Ⅱ)直线CB的斜率为2,所以所求切线的斜率为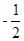 .………………10分
.………………10分
所求切线方程为: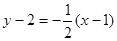 ,即
,即 ………………13分
………………13分
(1)设圆C的方程为(x-a)2+(y-b)2=r2,r>0,,依题意得:
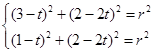
,解出待定系数,可得圆 C的方程.(2)当直线l的斜率存在时,可设直线l的方程,由圆心到直线的距离等于半径解出k值,从而得到直线l的方程.
解:(Ⅰ)方法1:设所求圆的方程为
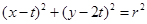 .依题意,可得………2分
.依题意,可得………2分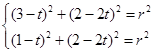 ,……………………4分
,……………………4分解得

∴所求圆的方程为
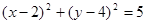 .…………………7分
.…………………7分方法2:由已知,AB的中垂线方程为:
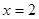 . …………………2分
. …………………2分由
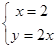 得
得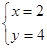 .所求圆的圆心为C(2,4).…………………………2分
.所求圆的圆心为C(2,4).…………………………2分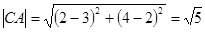 .
.∴所求圆的方程为
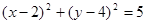 .……………………7分
.……………………7分(Ⅱ)直线CB的斜率为2,所以所求切线的斜率为
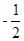 .………………10分
.………………10分所求切线方程为:
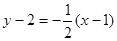 ,即
,即 ………………13分
………………13分
练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 相离,若
相离,若 能表示为某三角形的三条边长,则根据已知条件能够确定该三角形的形状是____________.
能表示为某三角形的三条边长,则根据已知条件能够确定该三角形的形状是____________.  ,斜率
,斜率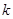 的直线
的直线 与椭圆相交于点
与椭圆相交于点 ,点
,点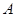 是线段
是线段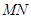 的中点,直线
的中点,直线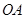 (
(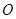 为坐标原点)的斜率是
为坐标原点)的斜率是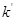 ,那么
,那么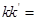
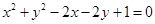 上的点到直线
上的点到直线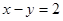 的距离的最大值是
的距离的最大值是 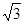 x-4的距离的最小值是 .
x-4的距离的最小值是 .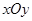 中,以
中,以 为圆心的圆与直线
为圆心的圆与直线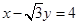 相切.
相切.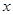 轴相交于
轴相交于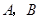 两点,圆内的动点
两点,圆内的动点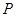 使
使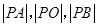 成等比数列,求
成等比数列,求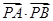 的取值范围.
的取值范围. 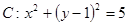 ,直线
,直线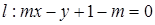
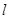 恒过定点;
恒过定点;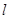 与圆交于
与圆交于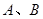 两点,若
两点,若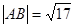 ,求直线
,求直线
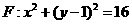 上运动,
上运动,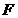 为圆心,线段AB的垂直平分线交BF于P.(1)求动点P的轨迹
为圆心,线段AB的垂直平分线交BF于P.(1)求动点P的轨迹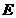 的方程;若曲线
的方程;若曲线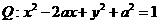 被轨迹
被轨迹 的最小值.(2)已知
的最小值.(2)已知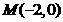 、
、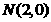 ,动点
,动点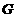 在圆
在圆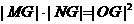 ,求
,求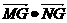 的取值范围.
的取值范围. 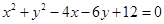 的位置关系是( )
的位置关系是( )