Question

【题目】如图，为了测量对岸A，B两点的距离，沿河岸选取C，D两点，测得CD=2km，∠CDB=∠ADB=30°，∠ACD=60°，∠ACB=45°，求A，B两点的距离．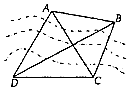

Answer 1

【答案】解：∠DAC=180°﹣∠ADB﹣∠BDC﹣∠ACD=60°，CD=2km
∴AC=2，
∠DBC=180°﹣∠BDC﹣∠ACD﹣∠ACB=45°
在△CDB中由正弦定理得：BC=
在△ABC中由余弦定理得：AB2=CB2+AC2﹣2CBACcos∠ACB=2，
∴AB= km．
答：A、B两点间的距离为 km．
【解析】根据题中条件先分别求出∠DAC，∠DBC．在△ADC中由正弦定理求得AD，在△CDB中由正弦定理求得DB，最后△ADB中由余弦定理求得AB．