题目内容
【题目】已知函数f（x）=e2x﹣ax2+bx﹣1，其中a，b∈R，e为自然对数的底数，若f（1）=0，f′（x）是f（x）的导函数，函数f′（x）在区间（0，1）内有两个零点，则a的取值范围是（ ）
A.（e2﹣3，e2+1）
B.（e2﹣3，+∞）
C.（﹣∞，2e2+2）
D.（2e2﹣6，2e2+2）
【答案】A
【解析】解：∵f（1）=0，∴e2﹣a﹣b﹣1=0，即b=e2﹣a﹣1， ∴f（x）=e2x﹣ax2+（e2﹣a﹣1）x﹣1，
∴f′（x）=2e2x﹣2ax+e2﹣a﹣1，
令f′（x）=0得2e2x=2ax+a+1﹣e2 ，
∵函数f′（x）在区间（0，1）内有两个零点，
∴y=2e2x与y=2ax+a+1﹣e2的函数图象在（0，1）上有两个交点，
作出y=2e2x与y=2ax+a+1﹣e2的函数图象，如图所示：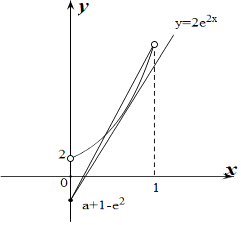
当a+1﹣e2≥2即a≥e2+1时，直线y=2ax与y=2e2x最多只有1个交点，不符合题意；
∴a+1﹣e2＜2，即a＜e2+1，
排除B，C，D．
故选A．
利用f（1）=0得出a，b的关系，根据f′（x）=0有两解可知y=2e2x与y=2ax+a+1﹣e2的函数图象在（0，1）上有两个交点，做出两函数图象，根据图象判断a的范围．
练习册系列答案
相关题目
【题目】某项科研活动共进行了5次试验，其数据如表所示：
特征量 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
x | 555 | 559 | 551 | 563 | 552 |
y | 601 | 605 | 597 | 599 | 598 |
（Ⅰ）从5次特征量y的试验数据中随机地抽取两个数据，求至少有一个大于600的概率；
（Ⅱ）求特征量y关于x的线性回归方程 
；并预测当特征量x为570时特征量y的值．
（附：回归直线的斜率和截距的最小二乘法估计公式分别为 
= 
， 
）
