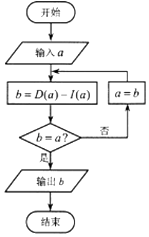
题目内容
【题目】递增数列1,3,4,9,10,12,13,…由一些正整数组成,它们要么是3的幂要么是若干个不同的3的幂的和.求第2014项的值.
【答案】88329
【解析】
记此数列为![]() .则
.则![]() .
.
用二进制表示项的序号n,三进制表示项![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
由题意,知![]() 的三进制表示各位仅可取0、1两个值且单调递增,由此可猜测当
的三进制表示各位仅可取0、1两个值且单调递增,由此可猜测当![]() 时,
时,![]() .
.
接下来用数学归纳法证明.
假设当![]() 时,命题成立.
时,命题成立.
则当![]() 时,其中,
时,其中,![]() ,必有整数
,必有整数![]() ,使
,使![]() 且
且![]() .
.
故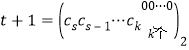 .
.
于是,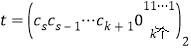 .
.
由假设得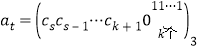 ,它是若干不同的3的幂之和且小于
,它是若干不同的3的幂之和且小于![]() 的最大值.
的最大值.
由![]() 单调递增知
单调递增知
![]()
![]() ,
,
其中,![]() .
.
则![]() ,
,
且![]() 仍为
仍为![]() 中某一项
中某一项![]() (当然
(当然![]() ).
).
于是![]() ,即
,即
![]() .
.
故![]()
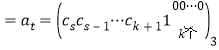 .
.
另一方面,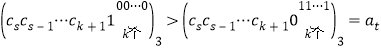 ,
,
当然 ,可表示为若干个互不相同的3的幂之和,故存在
,可表示为若干个互不相同的3的幂之和,故存在![]() ,使
,使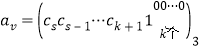 .
.
从而,![]() .
.
而![]() ,于是,
,于是,![]() ,即
,即![]() .
.
因此,![]() .
.
这导致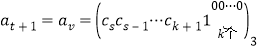 .
.
故当![]() 时,命题仍成立.
时,命题仍成立.
因为![]() ,所以,
,所以,
![]()
![]()
![]() .
.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目