题目内容
【题目】已知圆![]() ,A为圆O1上任意一点,点D在线段
,A为圆O1上任意一点,点D在线段![]() 上.
上.![]() ,已知
,已知![]() ,
,![]() .
.
(1)求点D的轨迹方程H;
(2)若直线![]() 与方程H所表示的图像交于E,F两点,
与方程H所表示的图像交于E,F两点,![]() 是椭圆
是椭圆![]() 上任意一点.若OG平分弦EF,且
上任意一点.若OG平分弦EF,且![]() ,
,![]() ,试判断四边形OEGF形状并证明.
,试判断四边形OEGF形状并证明.
【答案】(1)![]() ;(2)平行四边形,见解析
;(2)平行四边形,见解析
【解析】
(1)由题可得![]() ,得D的轨迹是以
,得D的轨迹是以![]() 为焦点的椭圆,求出
为焦点的椭圆,求出![]() ,可得轨迹方程;
,可得轨迹方程;
(2) 联立![]() ,利用韦达定理及弦长公式表示出
,利用韦达定理及弦长公式表示出![]() ,列方程求出
,列方程求出![]() 的值,进而可得EF平分OG,从而判断四边形OEGF形状.
的值,进而可得EF平分OG,从而判断四边形OEGF形状.
解:(1) ∵![]() ,
,
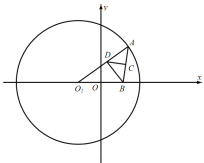
∴DC为AB中垂线,
∴![]() ,
,
∴![]() ,
,
∴D的轨迹是以![]() 为焦点的椭圆,且
为焦点的椭圆,且![]() ,
,
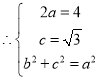 ,解得
,解得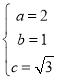 ,
,
∴点D轨迹方程H:![]() ;
;
(2)联立![]() ,
,![]() ,
,
设![]() ,
,
∵OG平分EF,
∴由中点弦公式有![]() ,①
,①
∴![]() ,
,
又G到EF距离为![]() ,
,
∴![]() ,
,
利用①以及![]() 有
有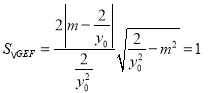 ,
,
化为![]() ,
,
令![]() ,则
,则![]() (*),观察有t = 1是一解,
(*),观察有t = 1是一解,
∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
又由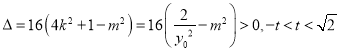 ,
,
∴![]() ,
,
∴方程(*)有唯一解t = 1即![]() ,
,
∴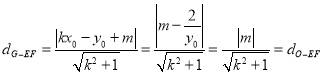 ,
,
∴EF也平分OG,
故四边形OEGF对角线相互平分,四边形OEGF是平行四边形

练习册系列答案
相关题目