题目内容
数列1,1+2,1+2+4,…,1+2+22+…+2n-1,…的前n项和Sn>1020,那么n的最小值是( )
| A.7 | B.8 | C.9 | D.10 |
D
∵1+2+22+…+2n-1=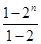 =2n-1,
=2n-1,
∴Sn=(2+22+…+2n)-n= -n=2n+1-2-n.
-n=2n+1-2-n.
若Sn>1020,则2n+1-2-n>1020,∴n≥10.
故选D项.
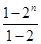 =2n-1,
=2n-1,∴Sn=(2+22+…+2n)-n=
 -n=2n+1-2-n.
-n=2n+1-2-n.若Sn>1020,则2n+1-2-n>1020,∴n≥10.
故选D项.

练习册系列答案
相关题目
 的前
的前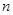 项和为
项和为 ,对任意的正整数
,对任意的正整数 成立,记
成立,记 .(1)(1)求数列
.(1)(1)求数列 的通项公式;
的通项公式; ,是否存在正整数
,是否存在正整数 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数 ,设数列
,设数列 的前
的前 ,求证:对于
,求证:对于 都有
都有
 ,则该数列前26项的和为________.
,则该数列前26项的和为________. )(n∈N*)均在函数y=
)(n∈N*)均在函数y= x+
x+ 且an=f(n)+f(n+1),则a1+a2+a3+…+a100等于( )
且an=f(n)+f(n+1),则a1+a2+a3+…+a100等于( )