题目内容
已知函数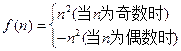 且an=f(n)+f(n+1),则a1+a2+a3+…+a100等于( )
且an=f(n)+f(n+1),则a1+a2+a3+…+a100等于( )
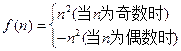 且an=f(n)+f(n+1),则a1+a2+a3+…+a100等于( )
且an=f(n)+f(n+1),则a1+a2+a3+…+a100等于( )| A.0 |
| B.100 |
| C.-100 |
| D.10200 |
B
由题意,a1+a2+a3+…+a100
=12-22-22+32+32-42-42+52+…+992-1002-1002+1012
=-(1+2)+(3+2)+…-(99+100)+(101+100)
=-(1+2+…+99+100)+(2+3+…+100+101)
=-1+101
=100,选B.
=12-22-22+32+32-42-42+52+…+992-1002-1002+1012
=-(1+2)+(3+2)+…-(99+100)+(101+100)
=-(1+2+…+99+100)+(2+3+…+100+101)
=-1+101
=100,选B.

练习册系列答案
相关题目
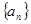 的前n项的和
的前n项的和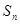 与
与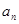 的关系是
的关系是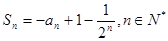 .
.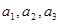 并归纳出数列
并归纳出数列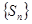 的前
的前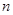 项和
项和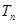 .
. 满足
满足 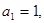 且对任意的
且对任意的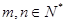 都有
都有 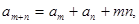 则
则 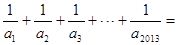 ( )
( )
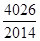
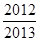

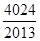
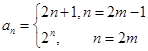 , m为正整数, 前n项和为
, m为正整数, 前n项和为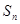 ,则
,则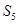 =____________.
=____________.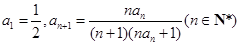 ,则数列{an}的前2012项的和为 .
,则数列{an}的前2012项的和为 .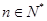 )个音符的音符串,要求由音符?开始,相邻两个音符不能相同.例如
)个音符的音符串,要求由音符?开始,相邻两个音符不能相同.例如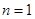 时,排除的音符串是?∮,??;
时,排除的音符串是?∮,??;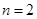 时排出的音符串是?∮?,?∮?,???,??∮,….记这种含
时排出的音符串是?∮?,?∮?,???,??∮,….记这种含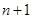 个音符的所有音符串中,排在最后一个的音符仍是?的音符串的个数为
个音符的所有音符串中,排在最后一个的音符仍是?的音符串的个数为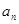 .故
.故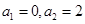 .则(1)
.则(1)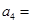 ;(2)
;(2)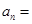 .
.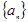 满足
满足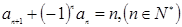 ,则数列
,则数列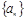 的前2016项的和
的前2016项的和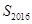 的值是___________.
的值是___________.