题目内容
【题目】设函数![]() .
.
(1)当![]() (
(![]() 为自然对数的底数)时,求
为自然对数的底数)时,求![]() 的最小值;
的最小值;
(2)讨论函数![]() 零点的个数;
零点的个数;
(3)若对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)2;(2)当![]() 时,函数
时,函数![]() 无零点;当
无零点;当![]() 或
或![]() 时,函数
时,函数![]() 有且仅有一个零点;当
有且仅有一个零点;当![]() 时,函数
时,函数![]() 有两个零点;(3)
有两个零点;(3)![]() .
.
【解析】
试题(1)当m=e时,![]() >0,由此利用导数性质能求出f(x)的极小值;(2)由
>0,由此利用导数性质能求出f(x)的极小值;(2)由![]() ,得
,得![]() ,令
,令![]() ,x>0,m∈R,则h(1)=
,x>0,m∈R,则h(1)=![]() ,
,
h′(x)=1-x2=(1+x)(1-x),由此利用导数性质能求出函数g(x)=f′(x)-![]() 零点的个数;(3)(理)当b>a>0时,f′(x)<1在(0,+∞)上恒成立,由此能求出m的取值范围
零点的个数;(3)(理)当b>a>0时,f′(x)<1在(0,+∞)上恒成立,由此能求出m的取值范围
试题解析:(1)由题设,当![]() 时,
时,![]()
易得函数![]() 的定义域为
的定义域为![]()
![]()
![]() 当
当![]() 时,
时,![]() ,此时
,此时![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,此时
,此时![]() 在
在![]() 上单调递增;
上单调递增;
![]() 当
当![]() 时,
时,![]() 取得极小值
取得极小值![]()
![]()
![]() 的极小值为2
的极小值为2
(2)![]() 函数
函数![]()
令![]() ,得
,得![]()
设![]()
![]()
当![]() 时,
时,![]() ,此时
,此时![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,此时
,此时![]() 在
在![]() 上单调递减;
上单调递减;
所以![]() 是
是![]() 的唯一极值点,且是极大值点,因此x=1也是
的唯一极值点,且是极大值点,因此x=1也是![]() 的最大值点,
的最大值点,
![]()
![]() 的最大值为
的最大值为![]()
又![]() ,结合y=
,结合y=![]() 的图像(如图),可知
的图像(如图),可知
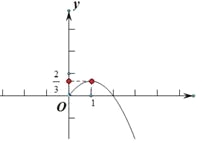
①当![]() 时,函数
时,函数![]() 无零点;
无零点;
②当![]() 时,函数
时,函数![]() 有且仅有一个零点;
有且仅有一个零点;
③当![]() 时,函数
时,函数![]() 有两个零点;
有两个零点;
④![]() 时,函数
时,函数![]() 有且只有一个零点;
有且只有一个零点;
综上所述,当![]() 时,函数
时,函数![]() 无零点;当
无零点;当![]() 或
或![]() 时,函数
时,函数![]() 有且仅有一个零点;当
有且仅有一个零点;当![]() 时,函数
时,函数![]() 有两个零点.
有两个零点.
(3)对任意![]() 恒成立,等价于
恒成立,等价于![]() 恒成立
恒成立
设![]() ,
,![]() 在
在![]() 上单调递减
上单调递减
![]() 在
在![]() 恒成立
恒成立
![]() 恒成立
恒成立
![]() (对
(对![]() ,
,![]() 仅在
仅在![]() 时成立),
时成立),![]() 的取值范围是
的取值范围是![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目