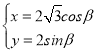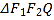题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)设函数![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(2)设函数![]() ,若
,若![]() 的图象与
的图象与![]() 的图象有
的图象有![]() ,
,![]() 两个不同的交点,证明:
两个不同的交点,证明:![]() .
.
【答案】(1)答案不唯一,具体见解析(2)证明见解析
【解析】
(1)求出![]() 的表达式并求导,分类讨论
的表达式并求导,分类讨论![]() 的单调性;(2)由题意可得
的单调性;(2)由题意可得![]() 有两个不同的根,则
有两个不同的根,则![]() ①,
①,![]() ②, 消去参数
②, 消去参数![]() 得
得![]() ,构造函数
,构造函数![]() 求导研究函数单调性并利用放缩法推出
求导研究函数单调性并利用放缩法推出![]() ,再次构造函数
,再次构造函数![]() ,通过证明
,通过证明![]() 来证明
来证明![]() .
.
(1)![]() ,定义域为
,定义域为![]() ,
,
![]() .
.
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
当![]() 时,令
时,令![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() ,
,![]() 上单调递增;
上单调递增;
令![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() 上单调递减.
上单调递减.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
当![]() 时,令
时,令![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() ,
,![]() 上单调递增;
上单调递增;
令![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() 上单调递减.
上单调递减.
(2)![]() ,
,
因为函数![]() 的图象与
的图象与![]() 的图象有两个不同的交点,
的图象有两个不同的交点,
所以关于![]() 的方程
的方程![]() ,即
,即![]() 有两个不同的根.
有两个不同的根.
由题知![]() ①,
①,![]() ②,
②,
①+②得![]() ③,
③,
②-①得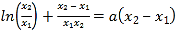 ④.
④.
由③,④得![]() ,不妨设
,不妨设![]() ,记
,记![]() .
.
令![]() ,则
,则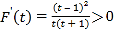 ,
,
所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
则![]() ,即
,即![]() ,所以
,所以![]() .
.
因为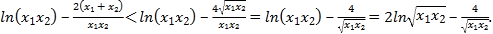
所以![]() ,即
,即![]() .
.
令![]() ,则
,则![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,所以
,所以![]() ,
,
即![]() ,所以
,所以![]() .
.
两边同时取对数可得![]() ,得证.
,得证.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某校倡导为特困学生募捐,要求在自动购水机处每购买一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出矿泉水箱数和收入情况,列表如下:
售出水量 | 7 | 6 | 6 | 5 | 6 |
收入 | 165 | 142 | 148 | 125 | 150 |
学校计划将捐款以奖学金的形式奖励给品学兼优的特困生,规定:特困生综合考核前20名,获一等奖学金500元;综合考核21-50名,获二等奖学金300元;综合考核50名以后的不获得奖学金.
(1)若![]() 与
与![]() 成线性相关,则某天售出9箱水时,预计收入为多少元?
成线性相关,则某天售出9箱水时,预计收入为多少元?
(2)假设甲、乙、丙三名学生均获奖,且各自获一等奖和二等奖的可能性相同,求三人获得奖学金之和不超过1000元的概率.
附:回归方程![]() ,其中
,其中 .
.