题目内容

3．将4位同学分到三个不同的班级，每个班级至少有一位同学，则不同的分法有（　　）
A．34种B．72种C．64种D．36种

分析 本题是一个分步计数问题，先选两个元素作为一个元素，问题变为三个元素在三个位置全排列，得到结果．

解答 解：由题意知本题是一个分步计数问题，
4位同学分到三个不同的班级，每个班级至少有一位同学，先选两个人作为一个整体，问题变为三个元素在三个位置全排列，
共有C42A33=36种结果，
故选：D．

点评 本题考查分步计数原理，是一个基础题，也是一个易错题，因为如果先排三个人，再排最后一个人，则会出现重复现象，注意不重不漏．

练习册系列答案
相关题目
13．已知向量$\overrightarrow{m}$=（2cosx+2$\sqrt{3}$sinx，1），向量$\overrightarrow{n}$=（cosx，-y），且$\overrightarrow{m}$⊥$\overrightarrow{n}$．
（Ⅰ）将y表示为x的函数f（x），并求f（x）的单调递增区间；
（Ⅱ）已知A，B，C分别为△ABC的三个内角，若f（$\frac{A}{2}$）=3，且sinBsinC=$\frac{3}{4}$，试判断△ABC的形状．
14．已知数列{an}满足a1=0，an+1=an+2n，则a2016等于（　　）
A．2016×2 017B．2015×2 016C．2014×2 015D．2016×2 016
11．以下判断正确的是（　　）
A．“b=0”是“函数f（x）=ax2+bx+c是偶函数”的充要条件．
B．命题“存在x∈R，x2+x-1＜0”的否定是“任意x∈R，x2+x-1＞0”
C．命题“在△ABC中，若A＞B则sinA＞sinB”的逆命题为假命题．
D．函数y=f（x）为R上的可导函数，则f′（x0）=0是x0为函数f（x）极值点的充要条件．
18．已知向量$\overrightarrow{a}$=（$\sqrt{2}sin$（$\frac{π}{4}+mx$），-$\sqrt{3}$），$\overrightarrow{b}$=（$\sqrt{2}$sin（$\frac{π}{4}$+mx），cos2mx）x∈R，m∈R，函数f（x）=$\overrightarrow{a}•\overrightarrow{b}$．
（Ⅰ）当m=1时，x$∈[\frac{π}{4}，\frac{π}{2}]$时，求f（x）的最大值和最小值；
（Ⅱ）当m=$\frac{nπ}{2}$时，若f（x）在区间[0，2015]恰有2015个零点，求整数n的所有取值．
8．数列$\frac{3}{2}，\frac{5}{3}，\frac{7}{4}，\frac{9}{5}$，…的一个通项公式为an=$\frac{2n+1}{n+1}$．
15．在一次某班42名学生参加课外篮球、排球兴趣小组（每人参加且只参加一个兴趣小组）的情况调查中，经统计得到如下2×2列联表：（单位：人）
  篮球 排球 总计
 男同学 166   22 
 女同学 8 12 20
 总计 24 18 42
通过计算得x2=4.852，则参加“篮球小组”与性别间有关系的可能性为（　　）
（下面临界值表供参考
 P（x2≥k） 0.05 0.01
 k 3.841 6.635
A．99%B．95%C．90%D．无关系
12．如图所示的流程图中，若输出的结果为3．则输入的x值为$\frac{3}{2}$或-3
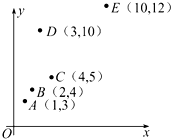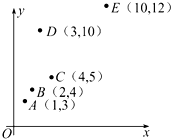13．有一散点图如图所示，在5个（x，y）数据中去掉D（3，10）后，下列说法正确的是（　　）
A．残差平方和变小
B．相关系数r变小
C．相关指数R2变小
D．解释变量x与预报变量y的相关性变弱

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网