题目内容
(本小题满分14分)
已知函数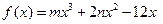 的减区间是
的减区间是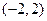 .
.
⑴试求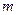 、
、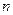 的值;
的值;
⑵求过点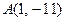 且与曲线
且与曲线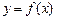 相切的切线方程;
相切的切线方程;
⑶过点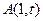 是否存在与曲线
是否存在与曲线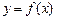 相切的3条切线,若存在,求实数t的取值范围;若不存在,请说明理由.
相切的3条切线,若存在,求实数t的取值范围;若不存在,请说明理由.
已知函数
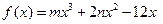 的减区间是
的减区间是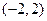 .
.⑴试求
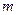 、
、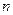 的值;
的值;⑵求过点
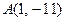 且与曲线
且与曲线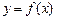 相切的切线方程;
相切的切线方程;⑶过点
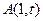 是否存在与曲线
是否存在与曲线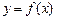 相切的3条切线,若存在,求实数t的取值范围;若不存在,请说明理由.
相切的3条切线,若存在,求实数t的取值范围;若不存在,请说明理由.解:⑴由题意知: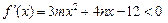 的解集为
的解集为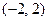 ,
,
所以,-2和2为方程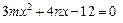 的根……2分
的根……2分
由韦达定理知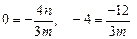 ,即m=1,n=0.……4分
,即m=1,n=0.……4分
⑵∵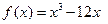 ,∴
,∴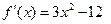 ,∵
,∵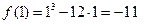
当A为切点时,切线的斜率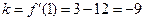 ,
,
∴切线为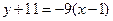 ,
,
即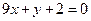 ; ……6分
; ……6分
当A不为切点时,设切点为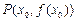 ,这时切线的斜率是
,这时切线的斜率是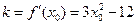 ,
,
切线方程为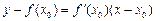 ,即
,即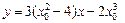
因为过点A(1,-11),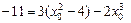 ,∴
,∴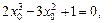
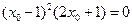 ,
,
∴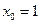 或
或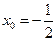 ,而
,而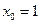 为A点,即另一个切点为
为A点,即另一个切点为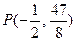 ,
,
∴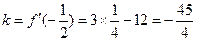 ,
,
切线方程为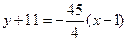 ,即
,即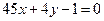 ………………8分
………………8分
所以,过点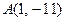 的切线为
的切线为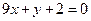 或
或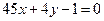 .…9分
.…9分
⑶存在满足条件的三条切线.
设点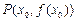 是曲线
是曲线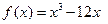 的切点,
的切点,
则在P点处的切线的方程为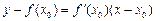 即
即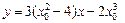
因为其过点A(1,t),所以,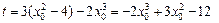 ,
,
由于有三条切线,所以方程应有3个实根, ……………11分
设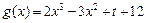 ,只要使曲线有3个零点即可.
,只要使曲线有3个零点即可.
因为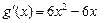 =0,∴
=0,∴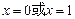 ,
,
当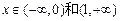 时
时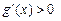 ,
,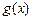 在
在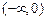 和
和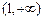 上单增,
上单增,
当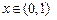 时
时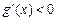 ,
,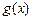 在
在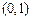 上单减,
上单减,
所以,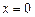 为极大值点,
为极大值点,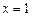 为极小值点.
为极小值点.
所以要使曲线与x轴有3个交点,当且仅当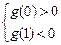 即
即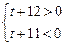 ,
,
解得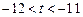 . ………14分
. ………14分
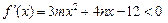 的解集为
的解集为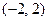 ,
,所以,-2和2为方程
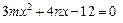 的根……2分
的根……2分由韦达定理知
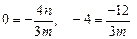 ,即m=1,n=0.……4分
,即m=1,n=0.……4分⑵∵
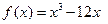 ,∴
,∴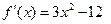 ,∵
,∵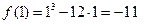
当A为切点时,切线的斜率
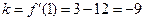 ,
,∴切线为
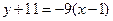 ,
,即
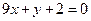 ; ……6分
; ……6分当A不为切点时,设切点为
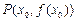 ,这时切线的斜率是
,这时切线的斜率是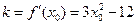 ,
,切线方程为
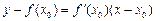 ,即
,即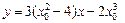
因为过点A(1,-11),
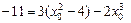 ,∴
,∴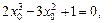
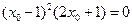 ,
,∴
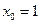 或
或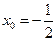 ,而
,而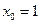 为A点,即另一个切点为
为A点,即另一个切点为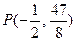 ,
,∴
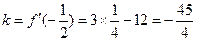 ,
,切线方程为
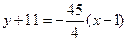 ,即
,即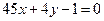 ………………8分
………………8分所以,过点
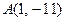 的切线为
的切线为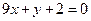 或
或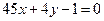 .…9分
.…9分⑶存在满足条件的三条切线.
设点
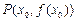 是曲线
是曲线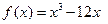 的切点,
的切点,则在P点处的切线的方程为
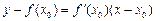 即
即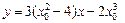
因为其过点A(1,t),所以,
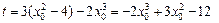 ,
, 由于有三条切线,所以方程应有3个实根, ……………11分
设
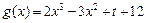 ,只要使曲线有3个零点即可.
,只要使曲线有3个零点即可.因为
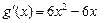 =0,∴
=0,∴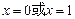 ,
,当
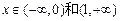 时
时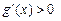 ,
,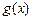 在
在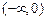 和
和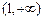 上单增,
上单增,当
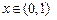 时
时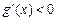 ,
,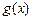 在
在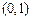 上单减,
上单减,所以,
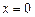 为极大值点,
为极大值点,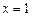 为极小值点.
为极小值点.所以要使曲线与x轴有3个交点,当且仅当
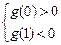 即
即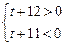 ,
,解得
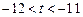 . ………14分
. ………14分略

练习册系列答案
相关题目
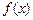 =
=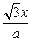 +
+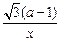 ,a≠0且a≠1.
,a≠0且a≠1.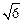 )上单调递减,在(
)上单调递减,在(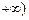 上单调递增,求a的值并写出函数的解析式;
上单调递增,求a的值并写出函数的解析式;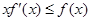 ,若
,若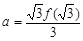 ,
,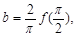
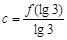 ,则
,则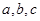 的大小关系是( )
的大小关系是( )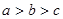
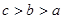
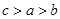
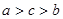
 (
( )(
)( 为自然对数的底数)
为自然对数的底数) 的极值
的极值 ,
, (
( )
)

 的方程
的方程 是否有解,并说明理由
是否有解,并说明理由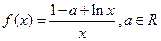 .
.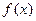 的极值;
的极值;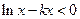 在
在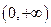 上恒成立,求
上恒成立,求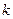 的取值范围;
的取值范围;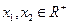 ,且
,且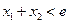 ,求证:
,求证: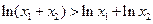 .
.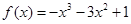 在
在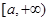 上的最大值为1,求a的取值范围( )
上的最大值为1,求a的取值范围( )



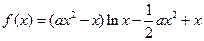 .
.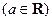 .
.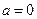 时,求曲线
时,求曲线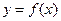 在
在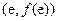 处的切线方程(
处的切线方程(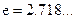 );
);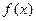 的单调区间.
的单调区间.