题目内容
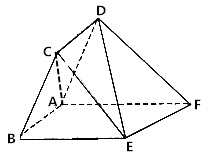
【题目】已知中心在原点、焦点在x轴上的椭圆C1与双曲线C2有共同的焦点，设左右焦点分别为F1，F2，P是C1与C2在第一象限的交点， 
PF1F2是以PF1为底边的等腰三角形，若椭圆与双曲线的离心率分别为e1，e2，则e1·e2的取值范围是( )
A. (
，+
) B. (
，+
) C. (
，+
) D. (0，+
)
【答案】A
【解析】∵中心在原点、焦点在x轴上的椭圆C1与双曲线C2有共同的焦点，
设左右焦点分别为F1，F2，P是C1与C2在第一象限的交点，△PF1F2是以PF1为底边的等腰三角形，
∴设椭圆和双曲线的长轴长分别为2a1，2a2，焦距为2c，
设|PF1|=x，|PF2|=|F1F2|=y，
由题意得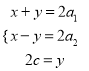
，
∵椭圆与双曲线的离心率分别为e1，e2，
∴e1e2=
，
由三角形三边关系得|F1F2|+|PF2|＞|PF1|＞|PF2|，
即2y＞x＞y，得到1＜
＜2，
∴1＜（
）2＜4，∴0＜（
）2﹣1＜3，
根据复合函数单调性得到e1e2=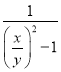
＞
．
故选A．
练习册系列答案
相关题目
