[题目]已知半径分别为 R .r 的两个圆外切于点 P . 点 P 到这两圆的一条外公切线的距离等于d .求证:. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知半径分别为 R 、r 的两个圆外切于点 P ，点 P 到这两圆的一条外公切线的距离等于d .求证：.

【答案】见解析

【解析】

如图，设半径为 R 的⊙O 与半径为r 的 ⊙O1 外切于点P ， AB 是两圆的一条外公切线， PC ⊥AB 于点 C.连结 OP 、O1 P ，则 O 、P 、 O1 共线.延长 BO1 交⊙O1 于点 D ，则 BD 是⊙O1的直径.连结AP 、PD .因为 OA ∥BD ，所以， ∠AOP =∠PO1D .因为△AOP 、△PO1D 都是等腰三角形，则有 ∠OPA =∠O1 PD .所以， A 、P 、D 三点共线.

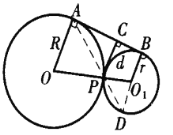
因为 PC∥DB ，所以，.

又因△AOP ∽△DO1P ，则有.

因此，.故，.

练习册系列答案

①f（x）=x﹣②f（x）=ex﹣1（e≈2.718，是一个重要常数）③f（x）=x+④y=x2

【题目】某校高一年级某次数学竞赛随机抽取100名学生的成绩，分组为[50，60），[60，70），[70，80），[80，90），[90，100]，统计后得到频率分布直方图如图所示：

（1）试估计这组样本数据的众数和中位数（结果精确到0.1）；

（2）年级决定在成绩[70，100]中用分层抽样抽取6人组成一个调研小组，对高一年级学生课外学习数学的情况做一个调查，则在[70，80），[80，90），[90，100]这三组分别抽取了多少人？

（3）现在要从（2）中抽取的6人中选出正副2个小组长，求成绩在[80，90）中至少有1人当选为正、副小组长的概率．

【题目】已知函数.

（1）求的单调区间；

（2）对任意的，，恒有，求正实数的取值范围.

【题目】下列命题中_________为真命题．

①“A∩B=A”成立的必要条件是“AB”； w ②“若x2+y2=0，则x，y全为0”的否命题；

③“全等三角形是相似三角形”的逆命题； ④“圆内接四边形对角互补”的逆否命题．

【题目】已知中心在原点、焦点在x轴上的椭圆C1与双曲线C2有共同的焦点，设左右焦点分别为F1，F2，P是C1与C2在第一象限的交点， PF1F2是以PF1为底边的等腰三角形，若椭圆与双曲线的离心率分别为e1，e2，则e1·e2的取值范围是( )

A. (，+) B. (，+) C. (，+) D. (0，+)

【题目】是定义在上的奇函数，其图象如图所示，令,则下列关于函数的叙述正确的是()

A. 若,则函数的图象关于原点对称

B. 若,则方程有大于2的实根

C. 若,则方程有两个实根

D. 若,则方程有两个实根

【题目】已知函数（x≠0，常数a∈R）．

（1）判断f（x）的奇偶性，并说明理由；

（2）若f（1）＝2，试判断f（x）在[2，＋∞）上的单调性

【题目】汽车租赁公司为了调查A，B两种车型的出租情况，现随机抽取了这两种车型各100辆汽车，分别统计了每辆车某个星期内的出租天数，统计数据如下表：
A型车

出租天数	1	2	3	4	5	6	7
车辆数	5	10	30	35	15	3	2

B型车

出租天数	1	2	3	4	5	6	7
车辆数	14	20	20	16	15	10	5

（1）从出租天数为3天的汽车（仅限A，B两种车型）中随机抽取一辆，估计这辆汽车恰好是A型车的概率；
（2）根据这个星期的统计数据，估计该公司一辆A型车，一辆B型车一周内合计出租天数恰好为4天的概率；
（3）如果两种车型每辆车每天出租获得的利润相同，该公司需要从A，B两种车型中购买一辆，请你根据所学的统计知识，给出建议应该购买哪一种车型，并说明你的理由．

试题分类