题目内容
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,
,![]() 是椭圆上关于原点
是椭圆上关于原点![]() 对称的两个动点,当点
对称的两个动点,当点![]() 的坐标为
的坐标为![]() 时,
时,![]() 的周长恰为
的周长恰为![]() .
.
(1)求椭圆的方程;
(2)过点![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 两点,且
两点,且![]()
![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)求出AB,得到a,然后求解b,即可得到椭圆方程;(2)当直线AB的斜率不存在时,求解三角形面积,设直线CD的方程为y=k(x+2)(k≠0).由![]() 消去y整理得:(1+2k2)x2+8k2x+8k2﹣8=0,△>0,设C(x1,y1),D(x2,y2),利用弦长公式求解CD,然后求解三角形面积,推出范围即可.
消去y整理得:(1+2k2)x2+8k2x+8k2﹣8=0,△>0,设C(x1,y1),D(x2,y2),利用弦长公式求解CD,然后求解三角形面积,推出范围即可.
(1)当点![]() 的坐标为
的坐标为![]() 时,
时,![]() ,所以
,所以![]() .
.
由对称性,![]() ,
,
所以![]() ,得
,得![]()
将点![]() 代入椭圆方程
代入椭圆方程![]() 中,解得
中,解得![]() ,
,
所以椭圆方程为![]() .
.
(2)当直线![]() 的斜率不存在时,
的斜率不存在时,![]() ,
,
此时![]() .
.
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() .
.
由![]() 消去
消去![]() 整理得:
整理得:![]() . 显然
. 显然![]() ,
,
设![]() ,则
,则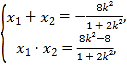
故![]()

![]()
![]() .
.
因为![]()
![]() ,所以
,所以![]() ,
,
所以点![]() 到直线
到直线![]() 的距离即为点
的距离即为点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
所以![]()
![]()
![]()
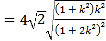
![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() .综上,
.综上,![]() .
.

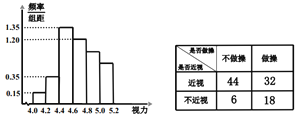
【题目】眼保健操是一种眼睛的保健体操,主要是通过按摩眼部穴位,调整眼及头部的血液循环,调节肌肉,改善眼的疲劳,达到预防近视等眼部疾病的目的.某学校为了调查推广眼保健操对改善学生视力的效果,在应届高三的全体800名学生中随机抽取了100名学生进行视力检查,并得到如图的频率分布直方图.
(1)若直方图中后三组的频数成等差数列,试估计全年级视力在5.0以上的人数;
(2)为了研究学生的视力与眼保健操是否有关系,对年级不做眼保健操和坚持做眼保健操的学生进行了调查,得到下表中数据,根据表中的数据,能否在犯错的概率不超过0.005的前提下认为视力与眼保健操有关系?
(3)在(2)中调查的100名学生中,按照分层抽样在不近视的学生中抽取8人,进一步调查他们良好的护眼习惯,在这8人中任取2人,记坚持做眼保健操的学生人数为X,求X的分布列和数学期望.
附:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |