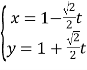题目内容
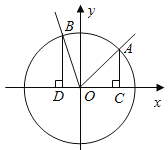
【题目】已知四棱锥![]() ,底面ABCD是边长为1的正方形,
,底面ABCD是边长为1的正方形,![]() ,平面
,平面![]() 平面ABCD,当点C到平面ABE的距离最大时,该四棱锥的体积为( )
平面ABCD,当点C到平面ABE的距离最大时,该四棱锥的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
【答案】B
【解析】
过点E作![]() ,垂足为H,过H作
,垂足为H,过H作![]() ,垂足为F,连接EF.因为
,垂足为F,连接EF.因为![]() 平面ABE,所以点C到平面ABE的距离等于点H到平面ABE的距离
平面ABE,所以点C到平面ABE的距离等于点H到平面ABE的距离![]() .设
.设![]() ,将
,将![]() 表示成关于
表示成关于![]() 的函数,再求函数的最值,即可得答案.
的函数,再求函数的最值,即可得答案.
过点E作![]() ,垂足为H,过H作
,垂足为H,过H作![]() ,垂足为F,连接EF.
,垂足为F,连接EF.
因为平面![]() 平面ABCD,所以
平面ABCD,所以![]() 平面ABCD,
平面ABCD,
所以![]() .
.
因为底面ABCD是边长为1的正方形,![]() ,所以
,所以![]() .
.
因为![]() 平面ABE,所以点C到平面ABE的距离等于点H到平面ABE的距离.
平面ABE,所以点C到平面ABE的距离等于点H到平面ABE的距离.
易证平面![]() 平面ABE,
平面ABE,
所以点H到平面ABE的距离,即为H到EF的距离![]() .
.
不妨设![]() ,则
,则![]() ,
,![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以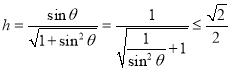 ,当
,当![]() 时,等号成立.
时,等号成立.
此时EH与ED重合,所以![]() ,
,![]() .
.
故选:B.


练习册系列答案
相关题目