题目内容
在直角梯形ABCD中,AB∥CD,AD⊥AB,CD=2AB=4,AD= ,E为CD的中点,将△BCE沿BE折起,使得CO⊥DE,其中垂足O在线段DE内.
,E为CD的中点,将△BCE沿BE折起,使得CO⊥DE,其中垂足O在线段DE内.

(1)求证:CO⊥平面ABED;
(2)问∠CEO(记为θ)多大时,三棱锥C-AOE的体积最大,最大值为多少.
(1)见解析(2) ,
,
【解析】(1)在直角梯形ABCD中,
CD=2AB,E为CD的中点,则AB=DE,
又AB∥DE,AD⊥AB,可知BE⊥CD.
在四棱锥C-ABED中,BE⊥DE,BE⊥CE,CE∩DE=E,CE,DE?平面CDE,
则BE⊥平面CDE.又BE?平面ABED,
所以平面ABED⊥平面CDE,
因为CO?平面CDE,
又CO⊥DE,且DE是平面ABED和平面CDE的相交直线,
故CO⊥平面ABED.
(2)由(1)知CO⊥平面ABED,
所以三棱锥C-AOE的体积V= S△AOE×OC=
S△AOE×OC= ×
× ×OE×AD×OC.
×OE×AD×OC.
由直角梯形ABCD中,CD=2AB=4,AD= ,CE=2.
,CE=2.
得在三棱锥C-AOE中,
OE=CEcos θ=2cos θ,OC=CEsin θ=2sin θ,
V= sin 2θ≤
sin 2θ≤ ,
,
当且仅当sin 2θ=1,θ∈ ,即θ=
,即θ= 时取等号(此时OE=
时取等号(此时OE= <DE,O落在线段DE内),
<DE,O落在线段DE内),
故当θ=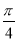 时,三棱锥C-AOE的体积最大,最大值为
时,三棱锥C-AOE的体积最大,最大值为 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目