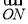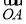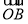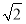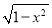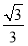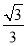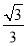题目内容
过正方形ABCD的顶点A，引PA⊥平面ABCD.若PA＝BA，则平面ABP和平面CDP所成的二面角的大小是( )．
A．30° B．45° C．60° D．90°
B
【解析】法一：建立如图(1)所示的空间直角坐标系，不难求出平面APB与平面PCD的法向量分别为n1＝(0,1,0)，n2＝(0,1,1)，故平面ABP与平面CDP所成二面角的余弦值为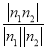
＝
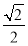，故所求的二面角的大小是45°.
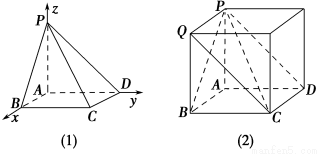
法二：将其补成正方体．如图(2)，不难发现平面ABP和平面CDP所成的二面角就是平面ABQP和平面CDPQ所成的二面角，其大小为45°.
练习册系列答案
相关题目
某种产品的广告费支出x与销售额y之间有如下对应数据(单位：百万元).
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | t | 70 |
根据上表提供的数据，求出y关于x的线性回归方程为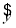
＝6.5x＋17.5，则表中t的值为________．
