题目内容
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 过坐标原点
过坐标原点![]() 且圆心在曲线
且圆心在曲线![]() 上.
上.
(1)若圆![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() (不同于原点
(不同于原点![]() ),求证:
),求证:![]() 的面积为定值;
的面积为定值;
(2)设直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,且
,且![]() ,求圆
,求圆![]() 的方程;
的方程;
(3)设直线![]() 与(2)中所求圆
与(2)中所求圆![]() 交于点
交于点![]() 、
、![]() ,
, ![]() 为直线
为直线![]() 上的动点,直线
上的动点,直线![]() ,
,![]() 与圆
与圆![]() 的另一个交点分别为
的另一个交点分别为![]() ,
,![]() ,且
,且![]() ,
,![]() 在直线
在直线![]() 异侧,求证:直线
异侧,求证:直线![]() 过定点,并求出定点坐标.
过定点,并求出定点坐标.
【答案】(1)证明过程见解析;(2) ![]() ;(3)直线
;(3)直线![]() 过定点
过定点![]() .
.
【解析】(1)由题意可设圆M的方程为![]() ,
,
即![]() .令
.令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() .
.
![]() (定值).
(定值).
(2)由![]() ,知
,知![]() .所以
.所以![]() ,解得
,解得![]() .
.
当![]() 时,圆心M
时,圆心M![]() 到直线
到直线![]() 的距离
的距离![]() 小于半径,符合题意;
小于半径,符合题意;
当![]() 时,圆心M
时,圆心M![]() 到直线
到直线![]() 的距离
的距离![]() 大于半径,不符合题意.
大于半径,不符合题意.
所以,所求圆M的方程为![]() .
.
(3)设![]() ,
,![]() ,
,![]() ,又知
,又知![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
显然![]() ,设
,设![]() ,则
,则![]() .
.
从而直线PE方程为:![]() ,与圆M的方程
,与圆M的方程![]() 联立,消去y,可得:
联立,消去y,可得:![]() ,所以,
,所以,![]() ,即
,即![]() ;
;
同理直线PF方程为:![]() ,与圆M的方程
,与圆M的方程![]() 联立,消去y,可得:
联立,消去y,可得:![]() ,所以,
,所以,![]() ,即
,即![]() .
.
所以![]()
![]() ;
;
![]()
![]() .
.
消去参数m整理得![]() . ①
. ①
设直线![]() 的方程为
的方程为![]() ,代入
,代入![]() ,
,
整理得![]() .
.
所以![]() ,
,![]() .
.
代入①式,并整理得![]() ,
,
即![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,过定点
,过定点![]() ;
;
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,过定点
,过定点![]()
第二种情况不合题意(因为![]() 在直径
在直径![]() 的异侧),舍去.
的异侧),舍去.
所以,直线![]() 过定点
过定点![]() .
.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案【题目】食品添加剂会引起血脂增高、血压增高、血糖增高等疾病,为了解三高疾病是否与性别有关,医院随机对入院的60人进行了问卷调查,得到了如下的列联表:
(1)请将列联表补充完整;若用分层抽样的方法在患三高疾病的人群中抽9人,其中女性抽几人?
患三高疾病 | 不患三高疾病 | 合计 | |
男 | 6 | 30 | |
女 | |||
合计 | 36 |
(2)为了研究三高疾病是否与性别有关,请计算出统计量![]() ,并说明你有多大把握认为患三高疾病与性别有关.
,并说明你有多大把握认为患三高疾病与性别有关.
下列的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() )
)
【题目】简阳羊肉汤已入选成都市级非遗项目,成为简阳的名片。当初向各地作了广告推广,同时广告对销售收益也有影响。在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
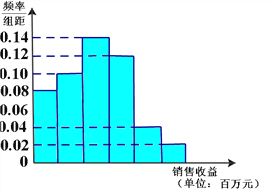
(Ⅰ)根据频率分布直方图,计算图中各小长方形的宽度;
(Ⅱ)根据频率分布直方图,估计投入4万元广告费用之后,并将各地销售收益的平均值(以各组的区间中点值代表该组的取值);
(Ⅲ)按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入x(单位:万元) | 1 | 2 | 3 | 4 | 5 |
销售收益y(单位:百万元) | 2 | 3 | 2 | 7 |
表中的数据显示,![]() 与
与![]() 之间存在线性相关关系,请将(Ⅱ)的结果填入空白栏,并计算
之间存在线性相关关系,请将(Ⅱ)的结果填入空白栏,并计算![]() 关于
关于![]() 的回归方程.回归直线的斜率和截距的最小二乘估计公式分别为
的回归方程.回归直线的斜率和截距的最小二乘估计公式分别为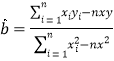 ,
,![]() .
.