题目内容
设椭圆
+
=1(a>b>0)的左右顶点分别为A,B,点P在椭圆上且异于A,B两点,O为坐标原点.
(1)若直线AP与BP的斜率之积为-
,求椭圆的离心率;
(2)若|AP|=|OA|,证明直线OP的斜率k满足|k|>
.
| x2 |
| a2 |
| y2 |
| b2 |
(1)若直线AP与BP的斜率之积为-
| 1 |
| 2 |
(2)若|AP|=|OA|,证明直线OP的斜率k满足|k|>
| 3 |
(1)设P(x0,y0),∴
+
=1①
∵椭圆
+
=1(a>b>0)的左右顶点分别为A,B,∴A(-a,0),B(a,0)
∴kAP=
,kBP=
∵直线AP与BP的斜率之积为-
,∴x02=a2-2y02
代入①并整理得(a2-2b2)y02=0
∵y0≠0,∴a2=2b2
∴e2=
=
∴e=
∴椭圆的离心率为
;
(2)证明:依题意,直线OP的方程为y=kx,设P(x0,kx0),∴
+
=1
∵a>b>0,kx0≠0,∴
+
<1
∴(1+k2)x02<a2②
∵|AP|=|OA|,A(-a,0),
∴(x0+a)2+k2x02=a2
∴(1+k2)x02+2ax0=0
∴x0=
代入②得(1+k2)(
)2<a2
∴k2>3
∴直线OP的斜率k满足|k|>
.
| x02 |
| a2 |
| y02 |
| b2 |
∵椭圆
| x2 |
| a2 |
| y2 |
| b2 |
∴kAP=
| y0 |
| x0+a |
| y0 |
| x0-a |
∵直线AP与BP的斜率之积为-
| 1 |
| 2 |
代入①并整理得(a2-2b2)y02=0
∵y0≠0,∴a2=2b2
∴e2=
| a2-b2 |
| a2 |
| 1 |
| 2 |
∴e=
| ||
| 2 |
∴椭圆的离心率为
| ||
| 2 |
(2)证明:依题意,直线OP的方程为y=kx,设P(x0,kx0),∴
| x02 |
| a2 |
| k2x02 |
| b2 |
∵a>b>0,kx0≠0,∴
| x02 |
| a2 |
| k2x02 |
| a2 |
∴(1+k2)x02<a2②
∵|AP|=|OA|,A(-a,0),
∴(x0+a)2+k2x02=a2
∴(1+k2)x02+2ax0=0
∴x0=
| -2a |
| 1+k2 |
代入②得(1+k2)(
| -2a |
| 1+k2 |
∴k2>3
∴直线OP的斜率k满足|k|>
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


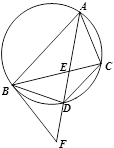
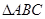 是圆的内接三角形,
是圆的内接三角形,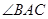 的平分线交圆于点
的平分线交圆于点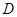 ,交
,交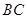 于点
于点 ,过点
,过点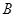 的圆的切线与
的圆的切线与 的延长线交于点
的延长线交于点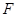 .在上述条件下,给出下列四个结论:
.在上述条件下,给出下列四个结论: