题目内容

直线l过抛物线y2=2px（p＞0）的焦点，且交抛物线于A，B两点，交其准线于C点，已知|AF|=4，
CB
=3
BF
，则p=（　　）
A．2B．
4
3
C．
8
3
D．4
过A，B分别作准线的垂线交准线于E，D．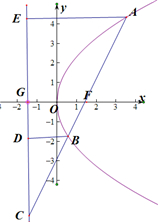
∵|AF|=4，
CB
=3
BF
，∴|AE|=4，|CB|=3|BF|，且|BF|=|BD|，
设|BF|=|BD|=a，则|BC|=3a，
根据三角形的相似性可得
|BD|
|AE|
=
|CB|
|AC|
，即
a
4
=
3a
3a+a+4
，解得a=2，
∴
|GF|
|AE|
=
|CF|
|AC|
，即
p
4
=
3a+a
3a+a+4
=
4a
4a+4
，
∴p=
4a
a+1
=
8
3
．
故选C．
练习册系列答案
相关题目
如图所示，△ABC内接于⊙O，AB＝AC，直线XY切⊙O于点C，BD∥XY，AC、BD相交于E.

(1)求证：△ABE≌△ACD； 
(2)若AB＝6 cm，BC＝4 cm，求AE的长．
直线l与双曲线
x2
2
-y2=1的同一支相交于A，B两点，线段AB的中点在直线y=2x上，则直线AB的斜率为（　　）
A．4B．2C．
1
2
D．
1
4
已知两点F′（-2，0），F（2，0），点P为坐标平面内的动点，且满足|
F′F
||
FP
|+
F′F
•
F′P
=0．
（1）求动点P（x，y）的轨迹C的方程；
（2）过点F的直线l与轨迹C和⊙F：（x-2）2+y2=1交于四点，自下而上依次记这四点为A、B、C、D，求
AB
•
CD
的最小值．
过抛物线y2=2px焦点F作直线l交抛物线于A，B两点，O为坐标原点，则△ABO为（　　）
A．锐角三角形B．直角三角形C．不确定D．钝角三角形
已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的左右焦点为F1（-c，0），F2（c，0），点Q是椭圆外的动点，满足|
F1Q
|=2a，点P是线段F1Q与该椭圆的交点
（1）若点P的横坐标为
a
2
，证明：|
F1P
|=a+
c
2

（2）若存在点Q，使得△F1QF2的面积等于b2，求椭圆离心率的取值范围．
如图，在平面直角坐标系xOy中，椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
3
2
，以原点为圆心，椭圆C的短半轴长为半径的圆与直线x-y+2=0相切．
（1）求椭圆C的方程；
（2）已知点P（0，1），Q（0，2）．设M，N是椭圆C上关于y轴对称的不同两点，直线PM与QN相交于点T，求证：点T在椭圆C上．
已知F1，F2分别为椭圆C1：
x2
b2
+
y2
a2
=1（a＞b＞0）的上下焦点，其F1是抛物线C2：x2=4y的焦点，点M是C1与C2在第二象限的交点，且|MF2|=
3
5
．
（1）试求椭圆C1的方程；
（2）与圆x2+（y+1）2=1相切的直线l：y=k（x+t）（t≠0）交椭圆于A，B两点，若椭圆上一点P满足
OA
+
OB
=λ
OP
，求实数λ的取值范围．
（200个•陕西）已知椭圆C：
x2
个2
+
y2
b2
=1（个＞b＞0）的离心率为
左
3
，短轴一个端点到右焦点的距离为
3
．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设直线l与椭圆C交于个、B两点，坐标原点O到直线l的距离为
3
2
，求△个OB面积的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网