题目内容
【题目】已知抛物线C:y2=2px(p>0)过点M(m,2),其焦点为F,且|MF|=2.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设E为y轴上异于原点的任意一点,过点E作不经过原点的两条直线分别与抛物线C和圆F:(x﹣1)2+y2=1相切,切点分别为A,B,求证:直线AB过定点F(1,0).
【答案】解:(Ⅰ)抛物线C的准线方程为: ![]() ,
,
∴ ![]() ,
,
又M在抛物线上,
即 ![]() ,
,
∴p2﹣4p+4=0,
解得p=2;
所以抛物线C的方程为y2=4x;
(Ⅱ)设点E(0,t)(t≠0),
由已知切线不为y轴,设EA:y=kx+t,
联立 ![]() ,消去y,
,消去y,
可得k2x2+(2kt﹣4)x+t2=0;
直线EA与抛物线C相切,
∴△=(2kt﹣4)2﹣4k2t2=0,
即kt=1代入 ![]() ,
,
∴x=t2 , 即A(t2 , 2t);
设切点B(x0 , y0),则由几何性质可以判断点O,B关于直线EF:y=﹣tx+t对称,
则 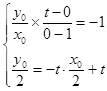 ,
,
解得:  ,
,
即 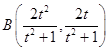 ;
;
思路1:直线AB的斜率为 ![]() ,
,
直线AB的方程为 ![]() ,
,
整理 ![]() ,
,
∴直线AB过定点恒过定点F(1,0);
当t=±1时,A(1,±2),B(1,±1),此时直线AB为x=1,过点F(1,0);
综上,直线AB过定点恒过定点F(1,0),
思路2:直线AF的斜率为 ![]() ,
,
直线BF的斜率为 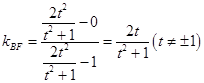 ,
,
∴kAF=kBF , 即A,B,F三点共线;
当t=±1时,A(1,±2),B(1,±1),此时A,B,F共线;
∴直线AB过定点F
【解析】(Ⅰ)根据抛物线的准线方程与M在抛物线上,列出方程组求出p的值即得抛物线方程;(Ⅱ)根据直线EA与圆锥曲线相切,用直线方程与圆锥曲线方程联立,△=0,根据圆的对称性,写出直线AB的方程;
思路1:利用直线AB的斜率、直线AB的方程,判断直线AB恒过定点;
思路2:根据三点共线以及直线的斜率,判断直线AB过定点F.

【题目】某企业有![]() 、
、![]() 两个岗位招聘大学毕业生,其中第一天收到这两个岗位投简历的大学生人数如下表:
两个岗位招聘大学毕业生,其中第一天收到这两个岗位投简历的大学生人数如下表:
|
| 总计 | |
女生 | 12 | 8 | 20 |
男生 | 24 | 56 | 80 |
总计 | 36 | 64 | 100 |
(1)根据以上数据判断是有![]() 的把握认为招聘的
的把握认为招聘的![]() 、
、![]() 两个岗位与性别有关?
两个岗位与性别有关?
(2)从投简历的女生中随机抽取两人,记其中投![]() 岗位的人数为
岗位的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
【题目】现从某医院中随机抽取了![]() 位医护人员的关爱患者考核分数(患者考核:
位医护人员的关爱患者考核分数(患者考核:![]() 分制),用相关的特征量
分制),用相关的特征量![]() 表示;医护专业知识考核分数(试卷考试:
表示;医护专业知识考核分数(试卷考试:![]() 分制),用相关的特征量
分制),用相关的特征量![]() 表示,数据如下表:
表示,数据如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的线性回归方程(计算结果精确到
的线性回归方程(计算结果精确到![]() );
);
(2)利用(1)中的线性回归方程,分析医护专业考核分数的变化对关爱患者考核分数的影响,并估计当某医护人员的医护专业知识考核分数为![]() 分时,他的关爱患者考核分数(精确到
分时,他的关爱患者考核分数(精确到![]() ).
).
参考公式及数据:回归直线方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为
 ,其中
,其中![]() .
.

