题目内容
如图:已知P是正方形ABCD所在平面外一点,点P在平面ABCD内的射影O是正方形的中心,PO=OD=a,E是PD的中点
(1)求证:PD⊥平面AEC
(2)求直线BP到平面AEC的距离
(3)求直线BC与平面AEC所成的角.
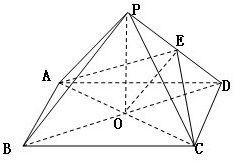
(1)求证:PD⊥平面AEC
(2)求直线BP到平面AEC的距离
(3)求直线BC与平面AEC所成的角.

证明:(1)∵PO⊥面ABCD,O为正方形ABCD的中心
∴PA=PB=PC=PD=AB=BC=CD=DA
∵E为PD的中点
∴PD⊥CE,PD⊥AE
又∵AE∩CE=E
∴PD⊥面AEC
(2)∵O、E是中点
∴OE∥PB
∴PB∥面AEC
直线PB与平面AEC的距离为P点到面AEC的距离
∵PD⊥面AEC
∴PE为P点到面AEC的距离为
a
(3)AD∥BCPD⊥面AEC
∴∠EAD为直线BC与面AEC所成的角为30°
∴PA=PB=PC=PD=AB=BC=CD=DA
∵E为PD的中点
∴PD⊥CE,PD⊥AE
又∵AE∩CE=E
∴PD⊥面AEC
(2)∵O、E是中点
∴OE∥PB
∴PB∥面AEC
直线PB与平面AEC的距离为P点到面AEC的距离
∵PD⊥面AEC
∴PE为P点到面AEC的距离为
| ||
| 2 |
(3)AD∥BCPD⊥面AEC
∴∠EAD为直线BC与面AEC所成的角为30°

练习册系列答案
相关题目