题目内容
已知二面角α-PQ-β为60°,点A和B分别在平面α和平面β内,点C在棱PQ上∠ACP=∠BCP=30°,CA=CB=a.
(1)求证:AB⊥PQ;
(2)求点B到平面α的距离;
(3)设R是线段CA上的一点,直线BR与平面α所成的角为45°,求CR的长.
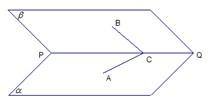
(1)求证:AB⊥PQ;
(2)求点B到平面α的距离;
(3)设R是线段CA上的一点,直线BR与平面α所成的角为45°,求CR的长.

证明:(1)作BM⊥PQ于M,连接AM,
∵∠ACP=∠BCP=30°,CA=CB=a,
∴△MBC≌△MAC,∴AM⊥PQ,PQ⊥平面ABM,AB?平面ABM,
∴AB⊥PQ.
(2)作BN⊥AM于N,
∵PQ⊥平面ABM,∴BN⊥PQ,
∴BN⊥α,BN是点B到平面α的距离,由(1)知∠BMA=60°,
∴BN=BMsin60°=CBsin30°sin60°=
.
∴点B到平面α的距离为
.
(3)连接NR,BR,∵BN⊥α,BR与平面α所成的角为∠BRN=45°,
RN=BN=
,CM=BCcos30°=
,
∴RN=
CM,∵∠BMA=60°,BM=AM,△BMA为正三角形,
N是BM中点,∴R是CB中点,∴CR=
.
∵∠ACP=∠BCP=30°,CA=CB=a,
∴△MBC≌△MAC,∴AM⊥PQ,PQ⊥平面ABM,AB?平面ABM,
∴AB⊥PQ.
(2)作BN⊥AM于N,
∵PQ⊥平面ABM,∴BN⊥PQ,
∴BN⊥α,BN是点B到平面α的距离,由(1)知∠BMA=60°,
∴BN=BMsin60°=CBsin30°sin60°=
| ||
| 4 |
∴点B到平面α的距离为
| ||
| 4 |
(3)连接NR,BR,∵BN⊥α,BR与平面α所成的角为∠BRN=45°,
RN=BN=
| ||
| 4 |
| ||
| 2 |
∴RN=
| 1 |
| 2 |
N是BM中点,∴R是CB中点,∴CR=
| a |
| 2 |

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
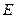 ,
,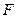 ,
,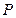 ,
,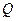 分别是棱长为
分别是棱长为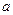 的正方体
的正方体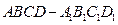 中
中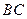 ,
,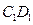 ,
,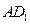 ,
, 的中点.
的中点. 平面
平面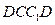 ;
;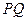 长;
长;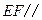 平面
平面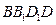 .
.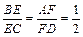 ,EF =
,EF =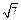 ,则直线AB和CD所成的角的大小是 .
,则直线AB和CD所成的角的大小是 .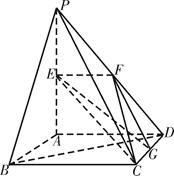 如图,平面
如图,平面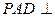 平面ABCD,
平面ABCD,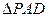 是直角三角形,
是直角三角形, ,E、F、G分别是
,E、F、G分别是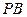 ∥面EFC;
∥面EFC;