题目内容
1.已知函数f(x)=sinx-$\sqrt{3}$cosx的定义域为[a,b],值域为[-1,2],则b-a的取值范围为( )| A. | $[\frac{2π}{3},\frac{4π}{3}]$ | B. | $[{\frac{5π}{6},2π}]$ | C. | $[{\frac{7π}{6},\frac{5π}{3}}]$ | D. | $[{\frac{7π}{6},2π}]$ |
分析 通过化简可得y=sin(x-$\frac{π}{3}$)∈[-$\frac{1}{2}$,1],画出其图象,即得结论.
解答 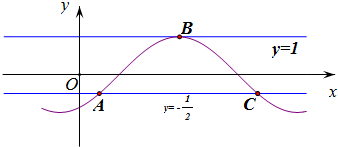 解:f(x)=sinx-$\sqrt{3}$cosx=2sin(x-$\frac{π}{3}$),
解:f(x)=sinx-$\sqrt{3}$cosx=2sin(x-$\frac{π}{3}$),
∵f(x)的值域为[-1,2],
∴y=sin(x-$\frac{π}{3}$)∈[-$\frac{1}{2}$,1],其图象如图:
其中A($\frac{π}{6}$,-$\frac{1}{2}$),B($\frac{5π}{6}$,1),C($\frac{3π}{2}$,-$\frac{1}{2}$),
∴b-a的最小值为:$\frac{5π}{6}$-$\frac{π}{6}$=$\frac{2π}{3}$,
b-a的最大值为:$\frac{3π}{2}$-$\frac{π}{6}$=$\frac{4π}{3}$,
即b-a的取值范围为:[$\frac{2π}{3}$,$\frac{4π}{3}$],
故选:A.
点评 本题考查三角函数的取值范围,注意解题方法的积累,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
12.用反证法证明命题:“a,b,c,d∈R,a+b=1,c+d=1,且ac+bd>1,则a,b,c,d中至少有一个负数”时的假设为( )
| A. | a,b,c,d全都大于等于0 | B. | a,b,c,d全为正数 | ||
| C. | a,b,c,d中至少有一个正数 | D. | a,b,c,d中至多有一个负数 |
6.曲线y=ex上的点到直线y=x的距离的最小值是( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{e}{2}$ | D. | $\frac{{\sqrt{e}}}{2}$ |