题目内容
11.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,若椭圆C上的一动点到右焦点的最短距离为$2-\sqrt{2}$,且右焦点到直线$x=\frac{a^2}{c}$的距离等于短半轴的长,已知P(4,0),过P的直线与椭圆交于M、N两点(Ⅰ)求椭圆C的方程
(Ⅱ)求$\overrightarrow{OM}•\overrightarrow{ON}$的取值范围.
分析 (Ⅰ)由题意知$\left\{\begin{array}{l}a-c=2-\sqrt{2}\\ \frac{a^2}{c}-c=b\end{array}\right.$,又a2=b2+c2.联立解出即可.
(II)由题意知直线MN的斜率存在,设直线MN的方程为y=k(x-4).与椭圆方程联立可得(2k2+1)x2-16k2x+32k2-4=0.由于△>0,可得${k^2}<\frac{1}{6}$.设点M(x1,y1),N(x2,y2),利用根与系数的关系及其数量积运算可得$\overrightarrow{OM}•\overrightarrow{ON}$=x1x2+y1y2=22-$\frac{26}{1+2{k}^{2}}$,即可得出.
解答 解:(Ⅰ)由题意知$\left\{\begin{array}{l}a-c=2-\sqrt{2}\\ \frac{a^2}{c}-c=b\end{array}\right.$,又a2=b2+c2.
解得$\left\{\begin{array}{l}a=2\\ b=\sqrt{2}\end{array}\right.$,
故椭圆C的方程$\frac{x^2}{4}+\frac{y^2}{2}=1$.
(Ⅱ)由题意知直线MN的斜率存在,设直线MN的方程为y=k(x-4).
由$\left\{\begin{array}{l}y=k(x-4)\\ \frac{x^2}{4}+\frac{y^2}{2}=1.\end{array}\right.$得(2k2+1)x2-16k2x+32k2-4=0.
$\begin{array}{l}△={(-16{k^2})^2}-4(2{k^2}+1)(32{k^2}-4)=16-96{k^2}>0\end{array}$,
∴${k^2}<\frac{1}{6}$.
设点M(x1,y1),N(x2,y2),
x1+x2=$\frac{16{k}^{2}}{1+2{k}^{2}}$,x1x2=$\frac{32{k}^{2}-4}{1+2{k}^{2}}$,
y1y2=k2(x1-4)(x2-4)=k2[x1x2-4(x1+x2)+16]=$\frac{12{k}^{2}}{1+2{k}^{2}}$,
∴$\overrightarrow{OM}•\overrightarrow{ON}$=x1x2+y1y2=$\frac{44{k}^{2}-4}{1+2{k}^{2}}$=22-$\frac{26}{1+2{k}^{2}}$,
∵$0≤{k^2}<\frac{1}{6}$,
∴$\overrightarrow{OM}•\overrightarrow{ON}∈[-4,\frac{5}{2})$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得△>0及其根与系数的关系、数量积运算性质,考查了推理能力与计算能力,属于难题.

 阅读快车系列答案
阅读快车系列答案| A. | $[\frac{2π}{3},\frac{4π}{3}]$ | B. | $[{\frac{5π}{6},2π}]$ | C. | $[{\frac{7π}{6},\frac{5π}{3}}]$ | D. | $[{\frac{7π}{6},2π}]$ |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
| A. | 6.5 | B. | 7 | C. | 7.5 | D. | 8 |
| A. | (-∞,4) | B. | (-4,4] | C. | (-∞,-4)∪[2,+∞) | D. | [-4,4) |
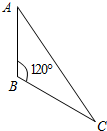 在△ABC中,AB=BC=4,∠ABC=120°,若把△ABC绕直线AB旋转一周,
在△ABC中,AB=BC=4,∠ABC=120°,若把△ABC绕直线AB旋转一周,