题目内容
9.已知f(x),g(x)都是定义在R上的函数,g(x)≠0,f′(x)g(x)-f(x)g′(x)>0,且f(x)=axg(x)(a>0a≠1),$\frac{f(1)}{g(1)}$+$\frac{f(-1)}{g(-1)}$=$\frac{5}{2}$.若数列$\frac{f(n)}{g(n)}$的前n项和小于126,则n的最大值为5.分析 f(x)=axg(x)(a>0,a≠1),可得ax=$\frac{f(x)}{g(x)}$.由于f′(x)g(x)-f(x)g′(x)>0,可得(ax)′=$\frac{{f}^{′}(x)g(x)-f(x){g}^{′}(x)}{{g}^{2}(x)}$>0,可得函数y=ax单调递增,a>1.由于$\frac{f(1)}{g(1)}$+$\frac{f(-1)}{g(-1)}$=$\frac{5}{2}$.解得a=2.由数列$\frac{f(n)}{g(n)}$的前n项和=2+22+…+2n,利用等比数列的前n项和公式即可得出.
解答 解:∵f(x)=axg(x)(a>0,a≠1),
∴ax=$\frac{f(x)}{g(x)}$.
∵f′(x)g(x)-f(x)g′(x)>0,
∴(ax)′=$\frac{{f}^{′}(x)g(x)-f(x){g}^{′}(x)}{{g}^{2}(x)}$>0,
∴函数y=ax单调递增,
∴a>1.
∵$\frac{f(1)}{g(1)}$+$\frac{f(-1)}{g(-1)}$=$\frac{5}{2}$.
∴a+a-1=$\frac{5}{2}$,a>1.
解得a=2.
若数列$\frac{f(n)}{g(n)}$的前n项和=2+22+…+2n=$\frac{2({2}^{n}-1)}{2-1}$=2n+1-2<126,
∴2n+1<27,
解得n<6,
∴满足条件的n的最大值为:5.
故答案为:5.
点评 本题考查了利用导数研究函数的单调性、等比数列的前n和公式,考查了推理能力与计算能力,属于难题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
4.已知函数f(x)=x3+mx2+nx+m2在x=1时有极值10,则m+n=( )
| A. | 7 | B. | 0 | C. | 0或-7 | D. | -7 |
1.已知函数f(x)=sinx-$\sqrt{3}$cosx的定义域为[a,b],值域为[-1,2],则b-a的取值范围为( )
| A. | $[\frac{2π}{3},\frac{4π}{3}]$ | B. | $[{\frac{5π}{6},2π}]$ | C. | $[{\frac{7π}{6},\frac{5π}{3}}]$ | D. | $[{\frac{7π}{6},2π}]$ |
19.如果点M(sinθ,cosθ)位于第二象限,那么角θ所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
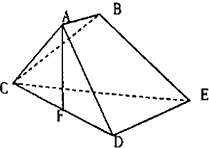 已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.
已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.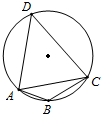 在半径为R的圆的内接四边形ABCD中,AB=2,BC=4,∠ABC=120°,AD+CD=10.求:
在半径为R的圆的内接四边形ABCD中,AB=2,BC=4,∠ABC=120°,AD+CD=10.求: