题目内容
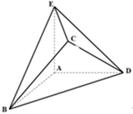
如图,在几何体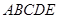 中,
中,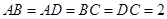 ,
,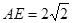 ,
,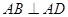 ,且
,且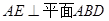 ,
,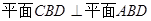 .
.
(I)求证: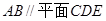 ;
;
(II)求二面角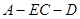 的余弦值.
的余弦值.
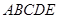 中,
中,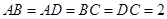 ,
,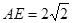 ,
,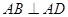 ,且
,且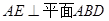 ,
,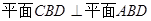 .
.
(I)求证:
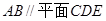 ;
;(II)求二面角
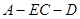 的余弦值.
的余弦值.(1)证明过程详见解析;(2)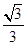 .
.
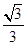 .
.试题分析:本题主要考查几何体中的线线平行与垂直的判定、线面平行与垂直的判定,以及空间向量法求二面角等数学知识,考查空间想象能力和逻辑思维能力,考查基本计算能力.第一问,利用已知的边长,得出
 与
与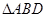 相似,从而得到
相似,从而得到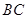 与
与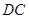 垂直,利用面面垂直的性质定理得
垂直,利用面面垂直的性质定理得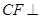 面
面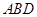 ,作出辅助线
,作出辅助线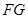 和
和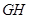 及
及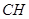 ,通过条件可得
,通过条件可得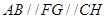 ,最后利用线面平行的判定证明
,最后利用线面平行的判定证明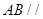 平面
平面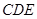 ;第二问,利用已知的垂直关系,建立如图的空间直角坐标系,写出各点的坐标,关键是求出平面
;第二问,利用已知的垂直关系,建立如图的空间直角坐标系,写出各点的坐标,关键是求出平面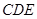 和平面
和平面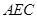 的法向量,利用夹角公式求出余弦值.
的法向量,利用夹角公式求出余弦值.试题解析:(I)
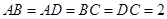
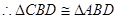 又
又
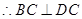 ,
,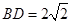
过点
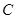 作
作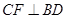 ,垂足为
,垂足为 ,则
,则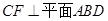 ,且
,且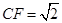 , 2分
, 2分过
 作
作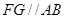 ,交
,交 于
于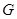 ,过
,过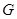 作
作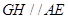 交
交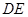 于
于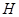 ,连结
,连结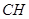 ,
,∵
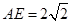 ,∴
,∴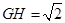 ,∴四边形
,∴四边形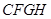 是平行四边形,
是平行四边形,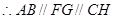 ,
,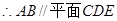 6分
6分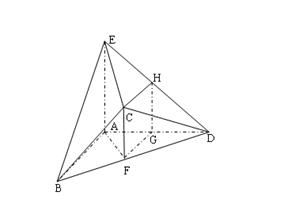
(II)如图建立空间直角坐标系,则
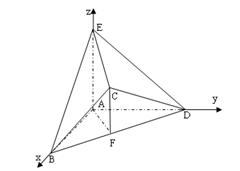
A(0,0,0),B(2,0,0),D(0,2,0),E(0,0,2
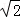 ),
),C(1,1,
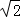 ),
),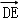 =(0,﹣2,2
=(0,﹣2,2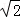 ),
),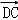 =(1,﹣1,
=(1,﹣1,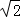 ), 8分
), 8分设平面CDE的一个法向量为
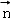 =(x,y,z),
=(x,y,z),则有
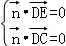 ,则﹣2y+2
,则﹣2y+2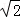 z=0,x﹣y+
z=0,x﹣y+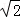 z=0,
z=0,取z=2,则y=2
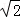 ,x=0,所以
,x=0,所以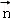 =(0,2
=(0,2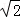 ,2), 10分
,2), 10分平面AEC的一个法向量为
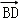 =(﹣2,2,0), 11分
=(﹣2,2,0), 11分故cos<
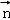 ,
,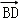 >=
>= 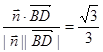 12分
12分
练习册系列答案
相关题目
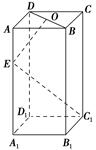
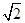 ,OE⊥EC1,求AA1的长.
,OE⊥EC1,求AA1的长.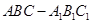 的底面是边长为
的底面是边长为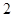 的正三角形,侧棱垂直于底面,侧棱长为
的正三角形,侧棱垂直于底面,侧棱长为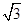 ,D为棱
,D为棱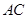 的中点。
的中点。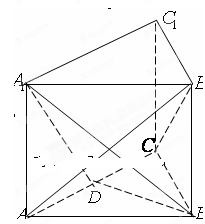
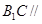 平面
平面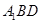 ;
;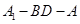 的大小.
的大小.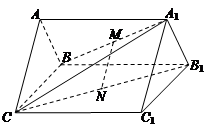
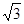 ,BC=2,求二面角A—A1C—B的余弦值的大小
,BC=2,求二面角A—A1C—B的余弦值的大小 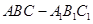 中,
中,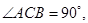
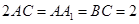 ,
,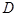 为
为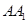 的中点
的中点
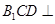 平面
平面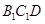 ;
;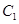 到平面
到平面 的距离.
的距离.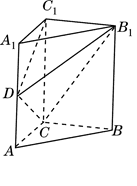
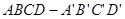 的外接球直径为
的外接球直径为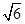 ,底面边长
,底面边长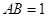 ,则侧棱
,则侧棱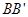 与平面
与平面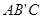 所成角的正切值为_________。
所成角的正切值为_________。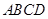 -
- 中,
中, 与平面ABCD所成角的余弦值为( )
与平面ABCD所成角的余弦值为( )