题目内容
如图,在直三棱柱ABC-A1B1C1中,点M是A1B的中点,点N是B1C的中点,连接MN
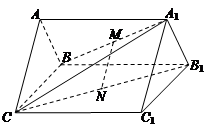
(Ⅰ)证明:MN//平面ABC;
(Ⅱ)若AB=1,AC=AA1=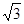 ,BC=2,求二面角A—A1C—B的余弦值的大小
,BC=2,求二面角A—A1C—B的余弦值的大小
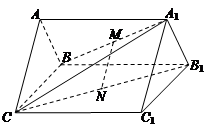
(Ⅰ)证明:MN//平面ABC;
(Ⅱ)若AB=1,AC=AA1=
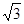 ,BC=2,求二面角A—A1C—B的余弦值的大小
,BC=2,求二面角A—A1C—B的余弦值的大小 (Ⅰ)详见解析;(Ⅱ)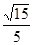 ;
;
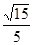 ;
;试题分析:(Ⅰ)主要利用线线平行可证线面平行;(Ⅱ)通过作平行线转化到三角形内解角;当然也可建系利用空间向量来解;
试题解析:(Ⅰ)证明:连接AB1,
∵四边形A1ABB1是矩形,点M是A1B的中点,
∴点M是AB1的中点;∵点N是B1C的中点,
∴MN//AC,∵MN
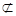 平面ABC,AC
平面ABC,AC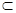 平面ABC,
平面ABC,∴MN//平面ABC 6分
(Ⅱ)解 :(方法一)如图,作
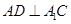 ,交
,交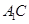 于点D,
于点D,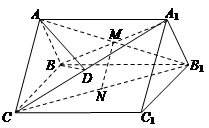
由条件可知D是
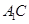 中点,连接BD,∵AB=1,AC=AA1=
中点,连接BD,∵AB=1,AC=AA1=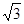 ,BC=2,
,BC=2,∴AB2+AC2= BC2,∴AB⊥AC,
∵AA1⊥AB,AA1∩AC=A,∴AB⊥平面
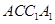
∴AB⊥A1C, ∴A1C⊥平面ABD,∴
 ∴
∴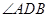 为二面角A—A1C—B的平面角,在
为二面角A—A1C—B的平面角,在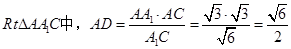 ,
, 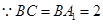 ,
, 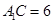 ,
, 在等腰
 中,
中,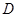 为
为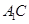 中点,
中点,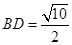 , ∴
, ∴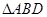 中,
中,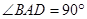 ,
, 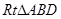 中,
中,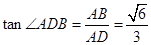 ,
, ∴二面角A—
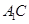 —B的余弦值是
—B的余弦值是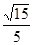 12分
12分(方法二)
 三棱柱
三棱柱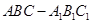 为直三棱柱,
为直三棱柱,∴
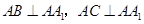 ,
,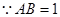 ,
,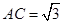 ,
,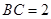 , ∴
, ∴ ,∴
,∴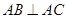
如图,建立空间直角坐标系,
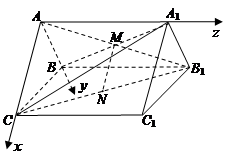
则A(0,0,0), B(0,1,0), C(
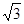 ,0,0), A1(0,0,
,0,0), A1(0,0,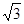 ),
),如图,可取
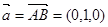 为平面
为平面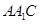 的法向量,
的法向量,设平面
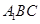 的法向量为
的法向量为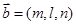 ,
,则
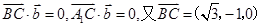 ,
,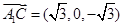 ,
,则由
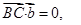
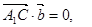 又
又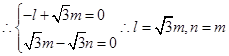 ,不妨取m=1,则
,不妨取m=1,则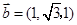 ,
,可求得
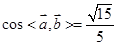 ,
, 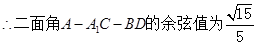 12分
12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
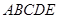 中,
中,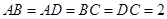 ,
,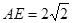 ,
,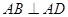 ,且
,且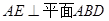 ,
,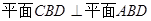 .
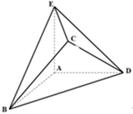
.
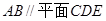 ;
;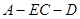 的余弦值.
的余弦值.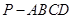 中,
中, ⊥底面
⊥底面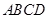 ,
,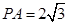 ,
, ,
,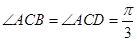 .
.
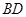 ⊥平面
⊥平面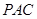 ;
; 上的点
上的点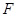 满足
满足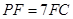 ,求三棱锥
,求三棱锥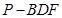 的体积.
的体积.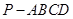 的底面
的底面 是正方形,棱
是正方形,棱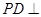 底面
底面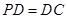 ,
,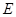 是
是 的中点.
的中点.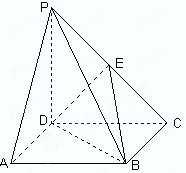
 平面
平面 ;
;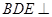 平面
平面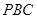 .
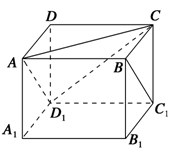
.
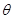 ,那么
,那么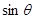 为 .
为 .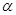 、
、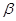 表示不同的平面,
表示不同的平面,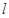 、
、 、
、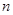 表示不同直线,则以下命题中正确的有 ( )
表示不同直线,则以下命题中正确的有 ( )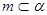 ,
,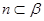 ,则
,则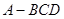 ,平面
,平面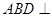 平面
平面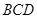 ,AB=AD=1,AB⊥AD,DB=DC,DB⊥DC
,AB=AD=1,AB⊥AD,DB=DC,DB⊥DC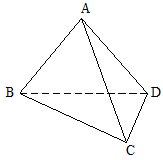
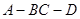 的正切值.
的正切值.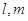 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,在下列条件中,能成为
是两个不同的平面,在下列条件中,能成为 的充分条件的是( )
的充分条件的是( ) ,
, 与
与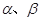 所成角相等
所成角相等 内的射影分别为
内的射影分别为 ,且
,且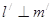
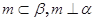
 ,
,