题目内容
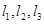 是空间三条不同的直线,则下列命题正确的是( )
是空间三条不同的直线,则下列命题正确的是( )A.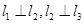 ,则 ,则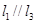 | B.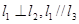 ,则 ,则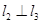 |
C.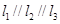 ,则 ,则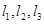 共面 共面 | D. 与 与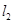 相交, 相交, 与 与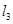 相交,则 相交,则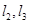 共面 共面 |
B
①反例正方体一个顶点的三条棱,A错;②异面直线所成角的定义,直线垂直定义,B对;③反例三棱柱的三条侧棱,C错;④反例正方体一个顶点的三条棱,D错。选B

练习册系列答案
相关题目
题目内容
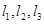 是空间三条不同的直线,则下列命题正确的是( )
是空间三条不同的直线,则下列命题正确的是( )A.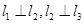 ,则 ,则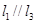 | B.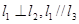 ,则 ,则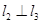 |
C.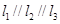 ,则 ,则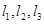 共面 共面 | D. 与 与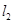 相交, 相交, 与 与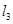 相交,则 相交,则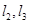 共面 共面 |
