题目内容
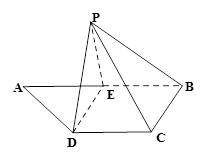
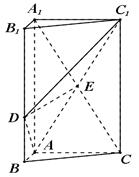
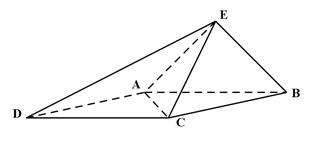
如图,三棱柱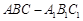 中,
中,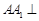 平面
平面 ,
,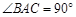 ,
,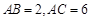 , 点
, 点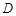 在线段
在线段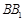 上,且
上,且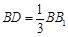 ,
,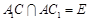 .
.
(Ⅰ)求证:直线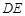 与平面
与平面 不平行;
不平行;
(Ⅱ)设平面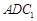 与平面
与平面 所成的锐二面角为
所成的锐二面角为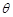 ,若
,若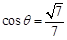 ,求
,求 的长;
的长;
(Ⅲ)在(Ⅱ)的条件下,设平面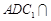 平面
平面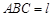 ,求直线
,求直线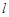 与
与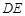 所成的角的余弦值.
所成的角的余弦值.
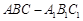 中,
中,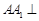 平面
平面 ,
,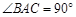 ,
,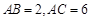 , 点
, 点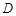 在线段
在线段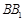 上,且
上,且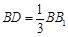 ,
,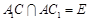 .
.
(Ⅰ)求证:直线
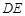 与平面
与平面 不平行;
不平行;(Ⅱ)设平面
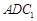 与平面
与平面 所成的锐二面角为
所成的锐二面角为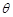 ,若
,若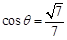 ,求
,求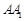 的长;
的长;(Ⅲ)在(Ⅱ)的条件下,设平面
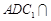 平面
平面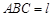 ,求直线
,求直线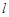 与
与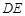 所成的角的余弦值.
所成的角的余弦值.(Ⅰ)见解析 (Ⅱ) 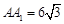 .(Ⅲ)直线
.(Ⅲ)直线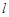 与
与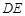 所成的角的余弦值为
所成的角的余弦值为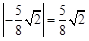 .
.
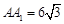 .(Ⅲ)直线
.(Ⅲ)直线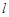 与
与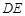 所成的角的余弦值为
所成的角的余弦值为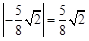 .
.(I)本小题易用空间向量法解决,易求出平面ABC的法向量,然后证明向量DE与平面ABC的法向量的数量积不等于零即可.
(2)先求出平面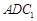 的一个法向量,然后
的一个法向量,然后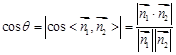 ,可以求出此直棱柱的高.
,可以求出此直棱柱的高.
(3)先找出平面平面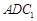 与平面
与平面 的交线.在平面
的交线.在平面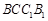 内,分别延长
内,分别延长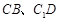 ,交于点
,交于点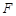 ,连结
,连结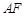 ,则直线
,则直线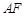 为平面
为平面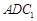 与平面
与平面 的交线.
的交线.
然后求出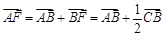 的坐标,再根据
的坐标,再根据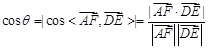 ,求出直线
,求出直线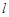 与
与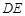 所成的角的余弦值.
所成的角的余弦值.
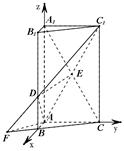
依题意,可建立如图所示的空间直角坐标系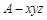 ,设
,设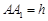 ,则
,则
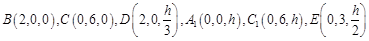 .2分
.2分
(Ⅰ)证明:由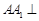 平面
平面 可知
可知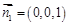 为平面
为平面 的一个法向量.
的一个法向量.
∴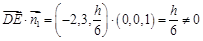 .∴ 直线
.∴ 直线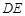 与平面
与平面 不平行. 4分
不平行. 4分
(Ⅱ)设平面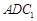 的法向量为
的法向量为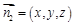 ,则
,则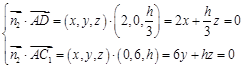 ,
,
取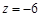 ,则
,则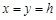 ,故
,故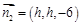 .6分
.6分
∴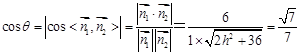 ,7分解得
,7分解得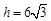 .∴
.∴ 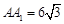 .
.
(Ⅲ)在平面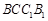 内,分别延长
内,分别延长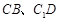 ,交于点
,交于点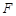 ,连结
,连结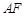 ,则直线
,则直线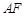 为平面
为平面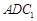 与平面
与平面 的交线.∵
的交线.∵ 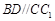 ,
,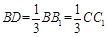 ,∴
,∴ 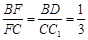 .∴
.∴ 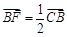 ,
,
∴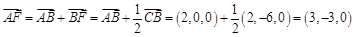 .········ 11分
.········ 11分
由(Ⅱ)知,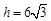 ,故
,故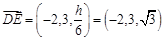 ,
,
∴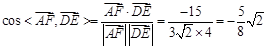 .∴ 直线
.∴ 直线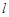 与
与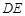 所成的角的余弦值为
所成的角的余弦值为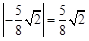
(2)先求出平面
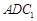 的一个法向量,然后
的一个法向量,然后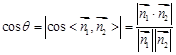 ,可以求出此直棱柱的高.
,可以求出此直棱柱的高.(3)先找出平面平面
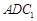 与平面
与平面 的交线.在平面
的交线.在平面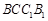 内,分别延长
内,分别延长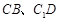 ,交于点
,交于点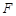 ,连结
,连结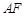 ,则直线
,则直线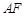 为平面
为平面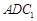 与平面
与平面 的交线.
的交线.然后求出
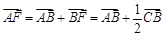 的坐标,再根据
的坐标,再根据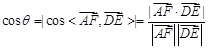 ,求出直线
,求出直线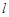 与
与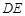 所成的角的余弦值.
所成的角的余弦值.依题意,可建立如图所示的空间直角坐标系
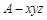 ,设
,设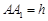 ,则
,则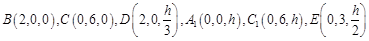 .2分
.2分
(Ⅰ)证明:由
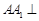 平面
平面 可知
可知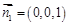 为平面
为平面 的一个法向量.
的一个法向量.∴
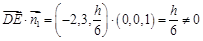 .∴ 直线
.∴ 直线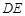 与平面
与平面 不平行. 4分
不平行. 4分(Ⅱ)设平面
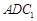 的法向量为
的法向量为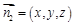 ,则
,则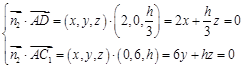 ,
,取
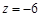 ,则
,则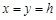 ,故
,故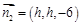 .6分
.6分∴
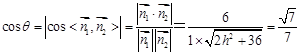 ,7分解得
,7分解得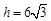 .∴
.∴ 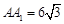 .
.(Ⅲ)在平面
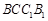 内,分别延长
内,分别延长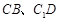 ,交于点
,交于点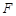 ,连结
,连结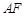 ,则直线
,则直线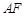 为平面
为平面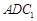 与平面
与平面 的交线.∵
的交线.∵ 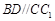 ,
,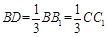 ,∴
,∴ 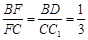 .∴
.∴ 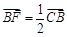 ,
,∴
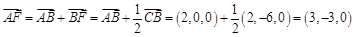 .········ 11分
.········ 11分由(Ⅱ)知,
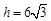 ,故
,故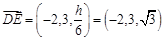 ,
,∴
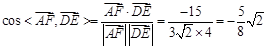 .∴ 直线
.∴ 直线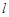 与
与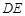 所成的角的余弦值为
所成的角的余弦值为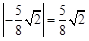

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
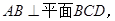 M、N分别是AC、AD的中点,BC
M、N分别是AC、AD的中点,BC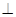 CD.
CD.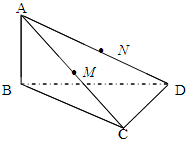
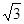 ,求直线AC与平面BCD所成的角.
,求直线AC与平面BCD所成的角.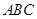 的边长为4,
的边长为4,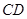 是
是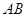 边上的高,
边上的高,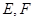 分别是
分别是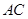 和
和 边的中点,现将△
边的中点,现将△ .
. 的位置关系,并说明理由;
的位置关系,并说明理由; 的余弦值;
的余弦值;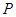 ,使
,使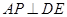 ?如果存在,求出
?如果存在,求出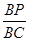 的值;如果不存在,请说明理由。
的值;如果不存在,请说明理由。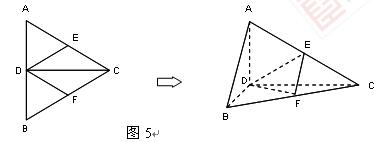
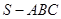 中,底面
中,底面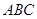 是边长为4的正三角形,平面
是边长为4的正三角形,平面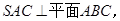
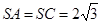 ,M,N分别为AB,SB的中点.
,M,N分别为AB,SB的中点.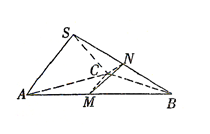
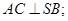
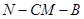 的余弦值.
的余弦值. 的底面为菱形,且
的底面为菱形,且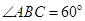 ,
,
 .
.
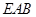
 平面
平面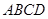 ;
; 的余弦值.
的余弦值.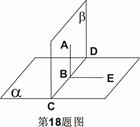
 ,
, 是不同的平面,
是不同的平面, ,
, 是不同的直线,给出下列命题:
是不同的直线,给出下列命题: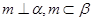 ,则
,则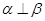 ;
;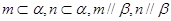 ,则
,则 ;
;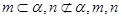 是异面直线,则
是异面直线,则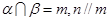 ,且
,且 ,则
,则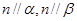 .
.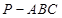 中,直线
中,直线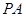 与
与 所成的角的大小为
所成的角的大小为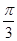
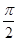
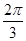
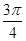
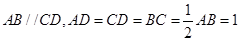 ,E为AB的中点,将
,E为AB的中点,将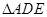 沿
沿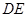 折起,使点A移至点P,若平面
折起,使点A移至点P,若平面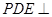 平面
平面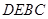 ,则D点到平面
,则D点到平面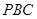 的距离是( )
的距离是( )