题目内容
【题目】已知一条曲线C在y轴右侧,曲线C上任意一点到点![]() 的距离减去它到y轴的距离都等于1.
的距离减去它到y轴的距离都等于1.
(1)求曲线C的方程;
(2)直线![]() 与轨迹C交于A,B两点,问:在x轴上是否存在定点
与轨迹C交于A,B两点,问:在x轴上是否存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 关于x轴对称而与直线
关于x轴对称而与直线![]() 的位置无关,若存在,求出点M的坐标,若不存在,请说明理由.
的位置无关,若存在,求出点M的坐标,若不存在,请说明理由.
【答案】(1)![]() (2)存在,
(2)存在,![]()
【解析】
(1)直接根据题意得到方程化简得到答案.
(2)设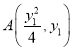 ,
,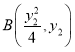 ,联立方程,根据韦达定理得到根与系数关系,计算
,联立方程,根据韦达定理得到根与系数关系,计算![]() ,化简整理得到答案.
,化简整理得到答案.
(1)设![]() 是曲线C上任意一点,那么点
是曲线C上任意一点,那么点![]() 满足:
满足:![]() ,
,
化简得![]() ,又因为曲线C在y轴右侧,故
,又因为曲线C在y轴右侧,故![]() ,
,
所以曲线C方程为:![]() .
.
(2)在x轴上存在定点![]() 使得直线
使得直线![]() 与
与![]() 关于x轴对称而与
关于x轴对称而与![]() 位置无关.
位置无关.
理由如下:
设直线![]() 与曲线C的交点坐标为
与曲线C的交点坐标为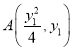 ,
,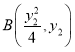 ,
,
由![]() ,消去x,整理得
,消去x,整理得![]() ,
,![]() ,
,
由韦达定理得![]() ,
,![]() ,.
,.
假设存在点![]() ,使得直线
,使得直线![]() 与
与![]() 关于x轴对称而与
关于x轴对称而与![]() 位置无关,
位置无关,
则![]() 对任意实数m恒成立,即
对任意实数m恒成立,即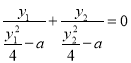 对任意实数m恒成立,
对任意实数m恒成立,
而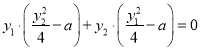 ,所以
,所以![]() ,
,
所以![]() ,又
,又![]() ,所以
,所以![]() .
.
故当![]() 对任意实数m,
对任意实数m,![]() ,
,
即在x轴上存在点![]() ,使得直线
,使得直线![]() 与
与![]() 关于x轴对称而与
关于x轴对称而与![]() 位置无关.
位置无关.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
【题目】英国统计学家E.H.辛普森1951年提出了著名的辛普森悖论,下面这个案例可以让我们感受到这个悖论.有甲乙两名法官,他们都在民事庭和行政庭主持审理案件,他们审理的部分案件被提出上诉.记录这些被上述案件的终审结果如下表所示(单位:件):
法官甲 | 法官乙 | ||||||
终审结果 | 民事庭 | 行政庭 | 合计 | 终审结果 | 民事庭 | 行政庭 | 合计 |
维持 | 29 | 100 | 129 | 维持 | 90 | 20 | 110 |
推翻 | 3 | 18 | 21 | 推翻 | 10 | 5 | 15 |
合计 | 32 | 118 | 150 | 合计 | 100 | 25 | 125 |
记甲法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为![]() ,
,![]() 和
和![]() ,记乙法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为
,记乙法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为![]() ,
,![]() 和
和![]() ,则下面说法正确的是
,则下面说法正确的是
A. ![]() ,
,![]() ,
,![]() B.
B. ![]() ,
,![]() ,
,![]()
C. ![]() ,
,![]() ,
,![]() D.
D. ![]() ,
,![]() ,
,![]()