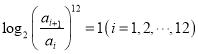题目内容
【题目】请从下面三个条件中任选一个，补充在下面的横线上，并解答．
①
②
③
的面积为
在中，内角A，B，C所对的边分别为a，b，c，已知b－c=2，cosA=
， ．
（1）求a；
（2）求
的值．
【答案】（1）不论选哪种条件，a=8（2）
【解析】
方案一：选择条件①：（1）首先利用向量的加法以及向量的数量积可得
，从而可求出
、
，然后再利用余弦定理即可求解.
（2）利用余弦定理可得
，再利用同角三角函数的基本关系求出
，由二倍角公式以及两角和的余弦公式即可求解.
方案二：选择条件②：（1）求出、，再利用余弦定理即可求解.
（2）同方案一
方案三：选择条件③：（1）利用同角三角函数的基本关系求出
，再利用三角形的面积公式可得
，求出、，再利用余弦定理即可求解.
（2）同方案一.
解：方案一：选择条件①：
（1）
∵
∴bc=24
由
解得
或
（舍去）
∴
∴a=8
（2）
∴
∴
∴
方案二：选择条件②：
（1）由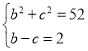
解得或（舍去）
∴
∴a=8
（2）同方案一
方案三：选择条件③：
（1）∵
∴
∴bc=24
由解得或（舍）
∴
∴a=8
（2）同方案一.
练习册系列答案
相关题目
