题目内容
点P是曲线 上的任意一点,则点P到直线y=x-2的最小距离为( )
上的任意一点,则点P到直线y=x-2的最小距离为( )
| A.1 | B. | C. | D. |
D
解析试题分析:曲线 是
是 的图象,对函数求导
的图象,对函数求导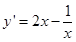 ,令
,令 ,那么
,那么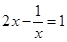 ,解得
,解得 (舍去),
(舍去),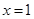 ,当
,当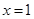 时,
时, ,切点为
,切点为 ,可得与直线y=x-2平行的切线方程为
,可得与直线y=x-2平行的切线方程为 ,两平行线间距离,即为所求最小距离,由两平行线间的距离公式可得
,两平行线间距离,即为所求最小距离,由两平行线间的距离公式可得 .
.
考点:1.导数的运算;2.两平行线间的距离公式;3.数形结合.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
若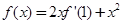 ,则
,则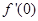 等于 ( )
等于 ( )
| A.-2 | B.-4 | C.2 | D.0 |
函数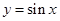 在点
在点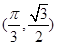 处的切线的斜率为( )
处的切线的斜率为( )
A. | B.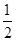 | C.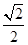 | D. |
已知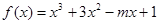 在
在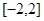 为单调增函数,则实数
为单调增函数,则实数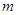 的取值范围为( )
的取值范围为( )
A.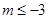 | B. | C.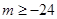 | D. |
设函数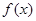 在R上存在导数
在R上存在导数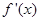 ,对任意的
,对任意的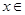 R,有
R,有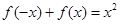 ,且
,且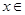 (0,+
(0,+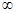 )时,
)时,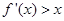 .若
.若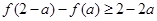 ,则实数a的取值范围为( )
,则实数a的取值范围为( )
| A.[1,+∞) | B.(-∞,1] | C.(-∞,2] | D.[2,+∞) |
曲线 与直线
与直线 所围成的封闭图形的面积为( )
所围成的封闭图形的面积为( )
A. | B. | C. | D. |
设函数 是
是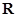 上以4为周期的可导偶函数,则曲线
上以4为周期的可导偶函数,则曲线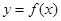 在
在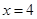 处的切线的斜率为( )
处的切线的斜率为( )
A.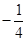 | B. | C.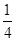 | D.4 |
已知 是可导的函数,且
是可导的函数,且 对于
对于 恒成立,则( )
恒成立,则( )
A. |
B. |
C. |
D. |
函数f(x)=ex-x(e为自然对数的底数)在区间[-1,1]上的最大值是( )
A.1+ | B.1 | C.e+1 | D.e-1 |