Question

【题目】2018年9月16日下午5时左右，今年第22号台风“山竹”在广东江门川岛镇附近正面登陆，给当地人民造成了巨大的财产损失，某记者调查了当地某小区的100户居民由于台风造成的经济损失，将收集的数据分成，，，，五组，并作出如下频率分布直方图.

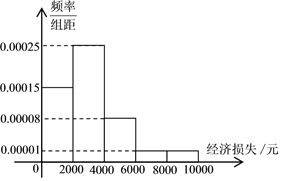
（Ⅰ）根据频率分布直方图估计该小区居民由于台风造成的经济损失的众数和平均值.

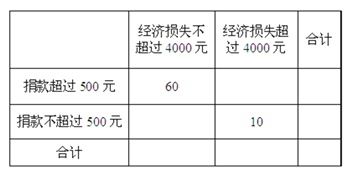
（Ⅱ）“一方有难，八方支援”，台风后居委会号召小区居民为台风重灾区捐款，记者调查的100户居民捐款情况如下表格，在表格空白处填写正确数字，并说明是否有99%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关？

（Ⅲ）将上述调查所得到的频率视为概率，现在从该地区大量受灾居民中，采用随机抽样方法每次抽取1户居民，抽取3次，记被抽取的3户居民中自身经济损失超过元的人数为，若每次抽取的结果是相互独立的，求的分布列及期望.

参考公式：，其中

Answer 1

【答案】（Ⅰ）众数为3000，平均值为2920（Ⅱ）没有把握（Ⅲ）详见解析

【解析】

（Ⅰ）最高矩形中点横坐标就是众数，每个矩形的中点横坐标与该矩形的纵坐标、组距相乘后求和可得平均值；（Ⅱ）根据直方图得到列联表，利用公式求得 ，与邻界值比较，即可得到结论；（Ⅲ）的取值可能有，根据独立重复试验概率公式求出各随机变量对应的概率，从而可得分布列，利用二项分布的期望公式可得结果.

（Ⅰ）根据频率分布直方图知该小区居民由于台风造成的经济损失的众数=3000（元）；

平均值=（元）

（Ⅱ）由频率分布直方图可知，在抽取的100人中，经济损失不超过元的有人，经济损失超过元的有100-80=20人，

则表格数据如下

	经济损失不 超过4000元	经济损失超 过4000元	合计
捐款超过500元	60	10	70
捐款不超过500元	20	10	30
合计	80	20	100

．

由于，

所以没有99%以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关．

（Ⅲ）由频率分布直方图可知抽到自身经济损失超过元居民的频率为，将频率视为概率. 由题意知的取值可能有，

	0	1	2	3

的分布列