题目内容
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() ,其右焦点为
,其右焦点为![]() .点
.点![]() 是椭圆
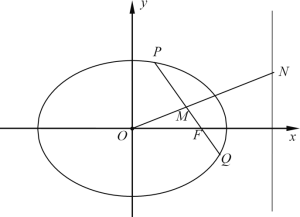
是椭圆![]() 上异于长轴端点的任意一点,连接
上异于长轴端点的任意一点,连接![]() 并延长交椭圆
并延长交椭圆![]() 于点
于点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,
,![]() 为坐标原点,且直线
为坐标原点,且直线![]() 与右准线
与右准线![]() 交于点
交于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() (2)
(2)![]() 或
或![]() .
.
【解析】
(1)由离心率得出a、b、c的等量关系,再将点A的坐标代入椭圆方程,可求出a、b、c的值,从而得出椭圆C的标准方程;(2)解法1:设点P(x0,y0)(y0≠0),对PF与x轴是否垂直进行分类讨论,在两种情况下求中点M的坐标,写出直线OM的方程,并求出点N的坐标,结合条件MN=2OM以及点P的坐标椭圆C的方程可求出点P的坐标;解法2:对直线PQ与x轴是否垂直进行分类讨论,在第一种情况PQ⊥x轴时,分别求出点M、N的坐标,并对条件MN=2OM进行验证是否满足题意;第二种情况就是直线PQ的斜率存在时,设直线PQ的方程为y=k(x﹣1)(k≠0),将直线PQ的方程与椭圆C的方程联立,列出韦达定理,并求出线段PQ的中点M的坐标,由MN=2ON得出k的值,从而得出点P的坐标.
(1)由题意可知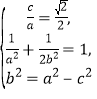 解得
解得![]() ,
,![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)法1:设![]() (
(![]() ).
).
当![]() 时,
时,![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ,
,![]() ,不符合题意;
,不符合题意;
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,代入
,代入![]() 的方程,消去
的方程,消去![]() 整理得
整理得
![]() ,
,
所以![]() 中点
中点![]() 的横坐标
的横坐标![]() ,因为
,因为![]() ,椭圆
,椭圆![]() 的右准线为
的右准线为![]() ,所以
,所以![]() ,从而
,从而![]() ,即
,即![]() . 又因为
. 又因为![]() ,所以
,所以![]() ,解得
,解得![]() 或
或![]() ,故点
,故点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
法2:当直线![]() 的斜率不存在时,
的斜率不存在时,![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ,
,![]() ,不符合题意;当直线
,不符合题意;当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() :
:![]() ,联立
,联立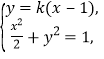 得
得
![]() ,所以
,所以![]() 中点
中点![]() 的横坐标
的横坐标![]() ,因为
,因为![]() ,椭圆
,椭圆![]() 的右准线为
的右准线为![]() ,所以
,所以![]() ,从而
,从而![]() ,解之得
,解之得![]() .当
.当![]() 时,
时,![]() :
:![]() ,联立
,联立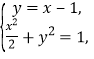 得
得![]() 或
或![]() ;
;
当![]() 时,
时,![]() :
:![]() ,联立
,联立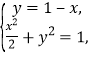 得
得![]() 或
或![]() .
.
故点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某学生对某小区30位居民的饮食习惯进行了一次调查,并用如图所示的茎叶图表示他们的饮食指数(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的,饮食以肉类为主).

(1)根据茎叶图,说明这30位居民中50岁以上的人的饮食习惯;
(2)根据以上数据完成如下2×2列联表;
主食蔬菜 | 主食肉类 | 总计 | |
50岁以下 | |||
50岁以上 | |||
总计 |
(3)能否有99%的把握认为居民的饮食习惯与年龄有关?
独立性检验的临界值表
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.