题目内容
圆
和
的位置关系是（ ）
| A．相离 | B．外切 | C．相交 | D．内切 |
D
解析试题分析：根据题意，由于圆的圆心（1,0），半径为1，和的圆心为（-2,0），半径为4，则可知圆心距d=3,而半径和为5，半径差为3，可知圆心距小于半径差，因此可知是两圆的相互内切，故选D.
考点：两圆的位置关系
点评:解决两圆的位置关系的关键是根据圆心距和半径和的关系来确定，属于基础题，也是重要的知识点。
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
直线
与圆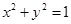
交于不同两点
、
，
为坐标原点，则“
”是“向量
、
满足
”的（ ）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
当曲线y=
与直线kx-y-2k+3=0有两个相异的交点时，实数k的取值范围是 ( )
A．(0, ) | B．( , ] | C．(,] | D．(,+∞) |
已知圆的方程为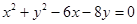
.设该圆过点H（3，5）的两条弦分别为AC和BD，且
.则四边形ABCD的面积最大值为（ ）
A． | B． | C．49 | D．50 |
圆
与直线
没有公共点的充分不必要条件是( )
A． | B． |
C． | D． |
若函数
的图象在x=0处的切线
与圆
相离，则
与圆C的位置关系是（ ）
| A．在圆外 | B．在圆内 | C．在圆上 | D．不能确定 |
已知圆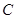
与直线
都相切，圆心在直线
上，则圆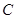的方程为（ ）
A． | B． |
C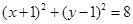． | D． |
圆
与圆
的位置关系为（ ）
| A．内切 | B．相交 | C．外切 | D．相离 |
已知圆
,
过点
的直线,则（ ）
A．与 相交 | B．与相切 |
| C．与相离 | D．以上三个选项均有可能 |