题目内容
已知各项均为正数的数列 满足:
满足: 。
。
(1)求 的通项公式
的通项公式
(2)当 时,求证:
时,求证:
(1) ,猜测:
,猜测: 。用数学归纳法证明。
。用数学归纳法证明。
(2)即证:
解析试题分析:(1) ,猜测:
,猜测: 。下用数学归纳法证明:
。下用数学归纳法证明:
①当 ,猜想成立;
,猜想成立;
②假设当 时猜想成立,即
时猜想成立,即 ,
,
由条件 ,
, ,
,
两式相减得: ,则当
,则当 时,
时, ,
, 时,猜想也成立。
时,猜想也成立。
故对一切的 成立。
成立。
(2) ,即证:
,即证:
对 ,令
,令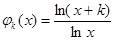 (
( ),则
),则 ,
,
显然 ,
, ,所以
,所以 ,
,
所以 ,
, 在
在 上单调递减.
上单调递减.
由 ,得
,得 ,即
,即 .
.
所以 ,
,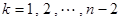 .
.
所以


 . 得证。
. 得证。
考点:本题主要考查数列的概念,数学归纳法的应用。
点评:难题,归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题。归纳推理问题,往往与数列知识相结合,需要综合应用数列的通项公式、求和公式等求解。本题利用数学归纳法证明不等式,对数学式子变形能力要求较高。

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 的前
的前 项和为
项和为 ,且
,且 ,
, .
. 的前
的前 ,且
,且 (
( 为常数),令
为常数),令 ,求数列
,求数列 的前
的前 。
。 的前
的前 项和为
项和为 ,
, ,且
,且 、
、 、
、 成等差数列.
成等差数列.  是一个首项为
是一个首项为 ,公差为
,公差为 的等差数列,求数列
的等差数列,求数列 的前
的前 .
. 为
为
 阶“期待数列”:
阶“期待数列”: ;②
;②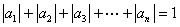 .
. 为
为 (
(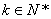 )阶“期待数列”,求公比
)阶“期待数列”,求公比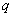 ;
;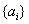 的前
的前 项和为
项和为 :
: ;
; 使
使 ,试问数列
,试问数列 能否为
能否为 是等差数列,
是等差数列,
 是否是等差数列,并说明理由;
是否是等差数列,并说明理由; ,试写出数列
,试写出数列 ,问是否存在这样的实数
,问是否存在这样的实数 ,使
,使 时取得最大值。若存在,求出
时取得最大值。若存在,求出 ,a1=1,点
,a1=1,点 在直线
在直线 上.
上. ,求证:
,求证: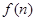 <1.
<1. 的前
的前 项和为
项和为 ,若对于任意的正整数
,若对于任意的正整数 ,
, ,求证:数列
,求证:数列 是等比数列,并求出
是等比数列,并求出 的前
的前 。
。 ,
, 为正整数.
为正整数. 和
和 的值;
的值; 的通项公式为
的通项公式为 (
( ),求数列
),求数列 ;
; 满足:
满足: ,
, ,设
,设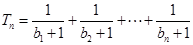 ,若(Ⅱ)中的
,若(Ⅱ)中的 恒成立,试求m的最大值.
恒成立,试求m的最大值. 的前n项和
的前n项和 (n为正整数)。
(n为正整数)。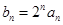 ,求证数列
,求证数列 是等差数列,并求数列
是等差数列,并求数列 ,
, 试比较
试比较 与
与 的大小,并予以证明。
的大小,并予以证明。