题目内容
设满足以下两个条件的有穷数列 为
为
 阶“期待数列”:
阶“期待数列”:
① ;②
;②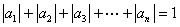 .
.
(1)若等比数列 为
为 (
(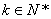 )阶“期待数列”,求公比
)阶“期待数列”,求公比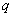 ;
;
(2)若一个等差数列 既是
既是 (
(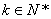 )阶“期待数列”又是递增数列,求该数列的通项公式;
)阶“期待数列”又是递增数列,求该数列的通项公式;
(3)记 阶“期待数列”
阶“期待数列”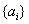 的前
的前 项和为
项和为 :
:
(ⅰ)求证: ;
;
(ⅱ)若存在 使
使 ,试问数列
,试问数列 能否为
能否为 阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
(1)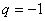 .(2)
.(2) .(3)(ⅰ)利用前n项和进行放缩证明.(ⅱ)数列
.(3)(ⅰ)利用前n项和进行放缩证明.(ⅱ)数列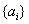 和数列
和数列
 不能为
不能为 阶“期待数列”.
阶“期待数列”.
解析试题分析:(1)若 ,则由①
,则由①
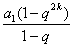 =0,得
=0,得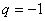 ,
,
由②得 或
或 .
.
若 ,由①得,
,由①得, ,得
,得 ,不可能.
,不可能.
综上所述,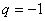 .
.
(2)设等差数列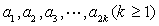 的公差为
的公差为 ,
, >0.
>0.
∵ ,∴
,∴ ,
,
∴ ,
,
∵ >0,由
>0,由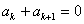 得
得 ,
, ,
,
由题中的①、②得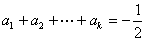 ,
, ,
,
两式相减得, , ∴
, ∴ ,
,
又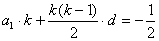 ,得
,得 ,
,
∴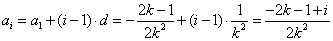 .
.
(3)记 ,
,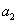 ,…,
,…, 中非负项和为
中非负项和为 ,负项和为
,负项和为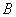 ,
,
则 ,
, ,得
,得 ,
, ,
,
(ⅰ) ,即
,即 .
.
(ⅱ)若存在 使
使 ,由前面的证明过程知:
,由前面的证明过程知: ,
, ,…,
,…,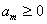 ,
,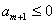 ,
, ,…,
,…, ,
,
且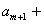
 …
…
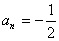 .
.
记数列
 的前
的前 项和为
项和为 ,
,
则由(ⅰ)知, ,
,
∴ =
=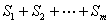
 ,而
,而 ,
,
∴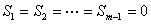 ,从而
,从而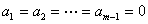 ,
, ,
,
又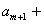
 …
…
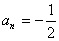 ,
,
则 ,
,
∴ ,
, 与
与 不能同时成立,
不能同时成立,
所以,对于有穷数列
 ,若存在
,若存在 使
使 ,则数列
,则数列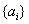

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
 的前
的前 项和为
项和为 ,若
,若 ,
, ,
, .
.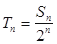 ,
, ;
; ,求
,求 的取值范围.
的取值范围.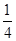 an bn,求数列{cn}的前n项和Tn.
an bn,求数列{cn}的前n项和Tn. 的前
的前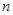 项和为
项和为 ,且对任意的
,且对任意的 都有
都有 ,
,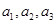 ;
; ,并用数学归纳法证明
,并用数学归纳法证明 为正常数,且
为正常数,且
 的通项公式;
的通项公式;
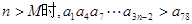 恒成立?若存在,求出相应的M的最小值;若不存在,请说明理由。
恒成立?若存在,求出相应的M的最小值;若不存在,请说明理由。 ,
, 满足:
满足: .
.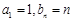 ,求数列
,求数列 ,且
,且 .
. ,求证:数列
,求证:数列 为等差数列;
为等差数列; 中任意一项的值均未在该数列中重复出现无数次,求首项
中任意一项的值均未在该数列中重复出现无数次,求首项 应满足的条件.
应满足的条件. 满足:
满足: 。
。 的通项公式
的通项公式 时,求证:
时,求证:
 的前
的前 项和为
项和为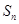 ,且
,且 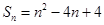 .
. ,数列
,数列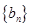 的前
的前 ,求证:
,求证: .
.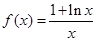 .
.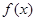 在区间
在区间 上有极值,求实数
上有极值,求实数 的取值范围;
的取值范围; 的方程
的方程 有实数解,求实数
有实数解,求实数 的取值范围;
的取值范围; ,
, 时,求证:
时,求证: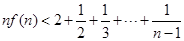 .
.