题目内容
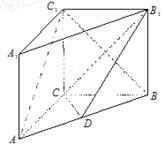
如图,长方体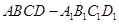 中
中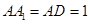 ,
,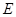 为
为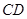 中点.
中点.
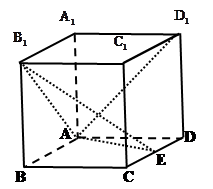
(1)求证: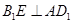 ;
;
(2)在棱上是否存在一点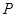 ,使得
,使得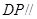 平面
平面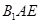 ?若存在,求
?若存在,求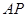 的长;若不存在,说明理由;
的长;若不存在,说明理由;
(3)若二面角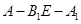 的大小为
的大小为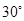 ,求
,求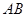 的长.
的长.
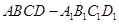 中
中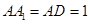 ,
,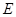 为
为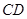 中点.
中点.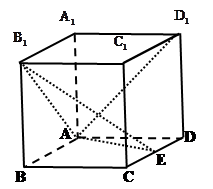
(1)求证:
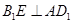 ;
;(2)在棱上是否存在一点
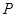 ,使得
,使得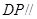 平面
平面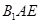 ?若存在,求
?若存在,求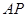 的长;若不存在,说明理由;
的长;若不存在,说明理由;(3)若二面角
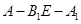 的大小为
的大小为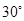 ,求
,求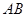 的长.
的长.(1)详见解析;(2)存在,且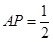 ;(3)
;(3)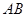 的长为
的长为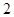 .
.
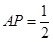 ;(3)
;(3)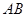 的长为
的长为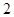 .
.试题分析:(1)以
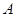 为原点,
为原点,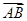 、
、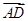 、
、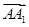 的方向为
的方向为 轴、
轴、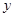 轴、
轴、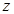 轴的正方向建立空间直角坐标系,并设
轴的正方向建立空间直角坐标系,并设 ,利用空间向量法证明
,利用空间向量法证明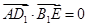 ,从而达到证明
,从而达到证明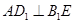 ;(2)设点
;(2)设点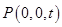 ,求出 平面
,求出 平面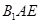 ,利用
,利用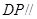 平面
平面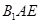 转化为
转化为 ,利用向量坐标运算求出
,利用向量坐标运算求出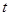 知,从而确定点
知,从而确定点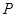 的坐标,最终得到
的坐标,最终得到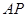 的长;(3)设
的长;(3)设 ,利用空间向量法求出二面角
,利用空间向量法求出二面角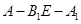 的余弦值的表达式,再结合二面角
的余弦值的表达式,再结合二面角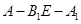 为
为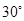 这一条件求出
这一条件求出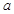 的值,从而确定
的值,从而确定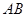 的长度.
的长度.试题解析:(1)以
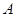 为原点,
为原点,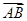 、
、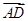 、
、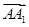 的方向为
的方向为 轴、
轴、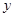 轴、
轴、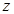 轴的正方向建立空间直角坐标系,
轴的正方向建立空间直角坐标系,设
 ,则
,则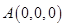 ,
,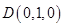 ,
,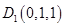 ,
,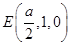 ,
,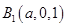 ,
,故
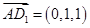 ,
,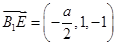 ,
,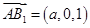 ,
,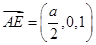 ,
,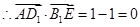 ,
,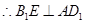 ;
;(2)假设在棱
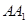 上存在一点
上存在一点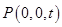 ,使得
,使得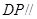 平面
平面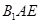 ,此时
,此时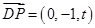 ,
,有设平面
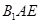 的法向量为
的法向量为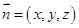 ,
,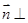 平面
平面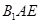 ,
,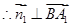 ,
,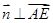 ,得
,得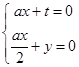 ,
,取
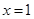 ,得平面
,得平面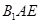 的一个法向量为
的一个法向量为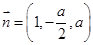 ,
,要使
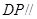 平面
平面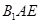 ,只要
,只要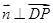 ,即有
,即有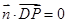 ,由此得
,由此得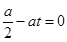 ,解得
,解得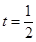 ,即
,即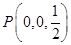 ,
,又
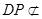 平面
平面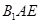 ,
,存在点
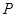 ,满足
,满足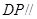 平面
平面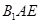 ,此时
,此时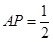 ;
;(3)连接
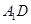 、
、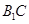 ,由长方体
,由长方体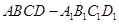 及
及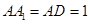 ,得
,得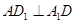 ,
,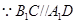 ,
,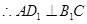 ,
,由(1)知,
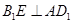 ,由
,由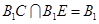 ,
,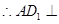 平面
平面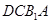 ,
,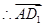 是平面
是平面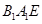 的一个法向量,此时
的一个法向量,此时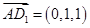 ,
,设
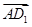 与
与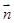 所成的角为
所成的角为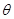 ,得
,得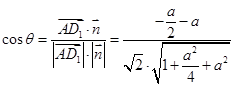 ,
,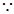 二面角
二面角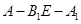 的大小为
的大小为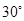 ,
,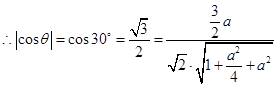 ,解得
,解得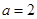 ,即
,即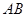 的长为
的长为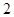 .
.
练习册系列答案
相关题目
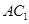 ∥平面
∥平面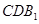 ;
;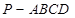 中,底面
中,底面 是直角梯形,
是直角梯形,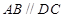 ,
,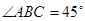 ,
,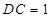 ,
,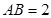 ,
,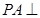 平面
平面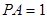 .
. 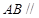 平面
平面 ;
; 平面
平面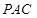 ;
;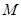 是
是 的中点,求三棱锥
的中点,求三棱锥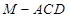 的体积.
的体积.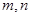 是两条不同的直线,
是两条不同的直线,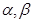 是两个不同的平面,则下列命题中的真命题是( )
是两个不同的平面,则下列命题中的真命题是( )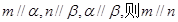
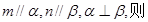
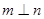
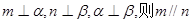
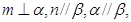 则
则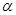 和
和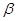 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题: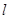 与
与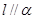 ;
;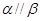 ;
;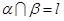 ,若
,若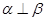 ;
;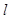 与平面
与平面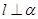 .
.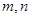 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,则下列命题正确的是( )
是两个不同的平面,则下列命题正确的是( )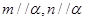 ,则
,则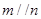
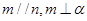 ,则
,则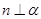
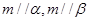 ,则
,则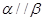
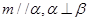 ,则
,则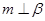
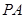 垂直于⊙
垂直于⊙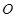 所在的平面,
所在的平面,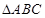 内接于⊙
内接于⊙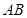 为⊙
为⊙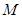 为线段
为线段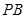 的中点.现有结论:①
的中点.现有结论:①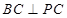 ;②
;② 平面
平面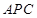 ;③点
;③点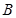 到平面
到平面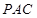 的距离等于线段
的距离等于线段 的长.其中正确的是( )
的长.其中正确的是( )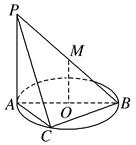
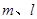 ,平面
,平面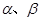 ,且
,且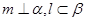 ,给出下列命题:
,给出下列命题: 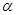 ∥
∥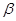 ,则m⊥
,则m⊥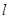 ; ②若
; ②若